题目内容
【题目】已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.
(1)求抛物线的解析式;
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使y1≥y2的x的取值范围.

【答案】(1) ![]() =-x+2x+3;(2)-1≤x≤2.
=-x+2x+3;(2)-1≤x≤2.
【解析】
(1)先根据抛物线与直线y2=x+1的一个交点的横坐标为2,可得交点坐标为(2,3),
再根据抛物线顶点坐标是(1,4), 设抛物线的解析式为y1=a(x-1)2+4,再把交点坐标(2,3),
代入抛物线解析式可得a=-1,继而可得抛物线解析式为:y1=-(x-1)2+4=-x2+2x+3.
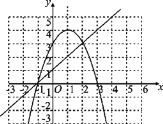
(2) 令y1=0,即-x2+2x+3=0,解得x1=3,x2=-1,因此抛物线与x轴交点坐标为(3,0)和(-1,0),在坐标系中画出抛物线与直线的图形如图所示,根据图象,可知使y1≥y2的x的取值范围为-1≤x≤2.
解:(1)∵抛物线与直线y2=x+1的一个交点的横坐标为2,
∴交点的纵坐标为2+1=3,即交点坐标为(2,3),
设抛物线的解析式为y1=a(x-1)2+4,把交点坐标(2,3)代入得:3=a(2-1)2+4,解得a=-1,∴抛物线解析式为:y1=-(x-1)2+4=-x2+2x+3.
(2)令y1=0,即-x2+2x+3=0,解得x1=3,x2=-1,
∴抛物线与x轴交点坐标为(3,0)和(-1,0),在坐标系中画出抛物线与直线的图形如图所示,
根据图象,可知使y1≥y2的x的取值范围为-1≤x≤2.

练习册系列答案
相关题目