题目内容
【题目】如图，在△ABC中，∠B=90°，BC=8 AB=6cm，动点P从点A开始沿边AB向点B以1cm/s的速度移动，动点Q从点B开始沿边BC向点C以2cm/s的速度移动．若P，Q两点分别从A，B两点同时出发，在运动过程中，△PBQ的最大面积是（ ）
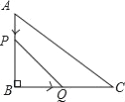
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
【答案】C
【解析】试题分析：先根据已知求边长BC，再根据点P和Q的速度表示BP和BQ的长，设△PBQ的面积为S，利用直角三角形的面积公式列关于S与t的函数关系式，并求最值即可．
∵tan∠C=
，AB=6cm， ∴
=
， ∴BC=8，
由题意得：AP=t，BP=6﹣t，BQ=2t，
设△PBQ的面积为S，则S=
×BP×BQ=×2t×（6﹣t），
S=﹣t2+6t=﹣（t2﹣6t+9﹣9）=﹣（t﹣3）2+9， P：0≤t≤6，Q：0≤t≤4，
∴当t=3时，S有最大值为9， 即当t=3时，△PBQ的最大面积为9cm2；
练习册系列答案
阅读快车系列答案
相关题目
