题目内容
【题目】如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
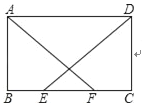
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
【答案】(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
【解析】
试题分析:(1)根据题中的已知条件我们不难得出:AB=CD,AF=DE,又因为BE=CF,那么两边都加上EF后,BF=CE,因此就构成了全等三角形的判定中边边边(SSS)的条件.
(2)由于四边形ABCD是平行四边形,只要证明其中一角为直角即可.
试题解析:证明:(1)∵BE=CF,BF=BE+EF,CE=CF+EF,
∴BF=CE.
∵四边形ABCD是平行四边形,
∴AB=DC.
在△ABF和△DCE中,
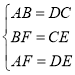 ,
,
∴△ABF≌△DCE(SSS).
(2)∵△ABF≌△DCE,
∴∠B=∠C.
∵四边形ABCD是平行四边形,
∴AB∥CD.
∴∠B+∠C=180°.
∴∠B=∠C=90°.
∴四边形ABCD是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了解某校计算机考试情况,抽取了50名学生的计算机考试成绩进行统计,统计结果如表所示,则50名学生计算机考试成绩的众数、中位数分别为( )
考试分数(分) | 20 | 16 | 12 | 8 |
人数 | 24 | 18 | 5 | 3 |
A. 20,16B. l6,20C. 20,l2D. 16,l2
【题目】七年级1班甲、乙两个小组的14名同学身高(单位:厘米)如下:
甲组 | 158 | 159 | 160 | 160 | 160 | 161 | 169 |
乙组 | 158 | 159 | 160 | 161 | 161 | 163 | 165 |
以下叙述错误的是( )
A. 甲组同学身高的众数是160 B. 乙组同学身高的中位数是161
C. 甲组同学身高的平均数是161 D. 两组相比,乙组同学身高的方差大