题目内容
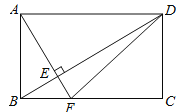
【题目】已知:如图,△ABC,∠ACB=90°,AC=5,DE⊥BD,BC=BD,∠ABE=∠CBD.

(1)求证:△ABC≌△EBD
(2)延长AC交DE于F点,若BC⊥BD,CF=4,求EF的长度.
【答案】(1)见解析(2)1
【解析】
(1)根据∠ABE=∠CBD得到∠ABC=∠EBD,再根据ASA即可证明△ABC≌△EBD;
(2)根据BC⊥BD,BC⊥AC,DE⊥BD得到四边形BCFD为矩形,再根据BC=BD得到矩形BCFD为正方形,故DF=CF,AC=DE,故可求解EF.
(1)∵∠ABE=∠CBD
∴∠ABE-∠EBC=∠CBD-∠EBC
∴∠ABC=∠EBD
又BC=BD,∠ACB=90°,DE⊥BD,
∴△ABC≌△EBD(ASA)
(2)∵BC⊥BD,BC⊥AC,DE⊥BD
∴四边形BCFD为矩形,
又BC=BD
∴矩形BCFD为正方形,
故DF=CF=4,AC=DE=5,
∴EF=DE-DF=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目