题目内容
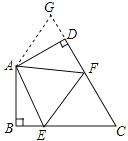
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图a,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
① 如图b,求证:BE⊥DQ;
② 如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由;
③ 若正方形ABCD的边长为10,DE=2,PB=PC,直接写出线段PB的长.

【答案】(1)证明见解析;(2)①证明见解析;②△DEP为等腰直角三角形,证明见解析;③PB=![]() 或
或![]()
【解析】(1)由旋转的性质得到∠BCP=∠DCQ,即可证明△BCP≌△DCQ;
(2)①由全等的性质和对顶角相等即可得到答案;
②由等边三角形的性质和旋转的性质求出∠EPD=45°,∠EDP=45°,即可判断△DEP的形状.
③由(1)结论,根据等腰三角形三线合一性质和相似三角形性质及勾股定理可得.
(1):如图a
证明:∵∠BCD=90°,∠PCQ=90°,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
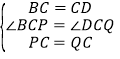 ,
,
∴△BCP≌△DCQ
(2)①如图b,∵△BCP≌△DCQ,
∴∠CBF=∠EDF,又∠BFC=∠DFE,
∴∠DEF=∠BCF=90°,
∴BE⊥DQ;
②△DEP为等腰直角三角形
∵△BCP为等边三角形,
∴∠BCP=60°,∴∠PCD=30°,又CP=CD,
∴∠CPDF=∠CDP=75°,又∠BPC=60°,∠CDQ=60°,
∴∠EPD=45°,∠EDP=45°,
∴△DEP为等腰直角三角形.
③PB= ![]() 或
或![]()

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目