题目内容
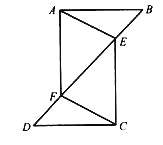
【题目】为丰富少年儿童的业余文化生活，某社区要在如图所示的AB所在的直线上建一图书阅览室，该社区有两所学校，所在的位置分别在点C和点D处。CA⊥AB于A，DB⊥AB于B，已知AB=25km，CA=15km,DB=10km,试问：阅览室E建在距A点多远时，才能使它到C、D两所学校的距离相等？
【答案】10 km
【解析】
把具体的位置关系转化成数学几何模型，找到等量关系，再设未知数，求出未知量即可.
解：设阅览室E到A的距离为x㎞．连结CE、DE．
在Rt△EAC和Rt△EBD中，
CE2=AE2+AC2=x2+152，
DE2=EB2+DB2=（25-x）2+102．
因为点E到点CD的距离，所以CE=DE．
所以CE2=DE2．即x2+152=(25-x)2+102．
所以x=10．
因此，阅览室E应建在距A点10km处.
【题目】有
筐白菜,以每筐
千克为标准,超过或不足的分别用正、负来表示,记录如下：
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,筐白菜总计超过或不足多少千克？
(2)若白菜每千克售价
元,则出售这筐白菜可卖多少元？
【题目】今年5月13日是“母亲节”，某校开展“感恩母亲，做点家务”活动为了了解同学们在母亲节这一天做家务情况，学校随机抽查了部分同学，并用得到的数据制成如下不完整的统计表：
做家务时间（小时） | 人数 | 所占百分比 |
A组：0.5 | 15 | 30% |
B组：1 | 30 | 60% |
C组：1.5 | x | 4% |
D组：2 | 3 | 6% |
合计 | y | 100 |
（1）统计表中的x= ，y= ；
（2）小君计算被抽查同学做家务时间的平均数是这样的：
第一步：计算平均数的公式是
，
第二步：该问题中n=4，x1=0.5，x2=1，x3=1.5，x4=2，
第三步：
=1.25（小时）
小君计算的过程正确吗？如果不正确，请你计算出正确的做家务时间的平均数；
（3）现从C，D两组中任选2人，求这2人都在D组中的概率（用树形图法或列表法）．
