题目内容
【题目】如图,在长方形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,下列结论:①△ABD≌△CDB;②∠BFE=∠BDC;③S△ABE=S△DEF;④AB=6,AD=8,DB=10,则AE=4.其中正确的个数为( )
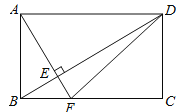
A.1个B.2个C.3个D.4个
【答案】C
【解析】
在长方形ABCD中有AB=CD,AD=CB,BD=DB,根据SSS可证△ABD≌△CDB,①正确;根据同角的余角相等可证∠BFE=∠BDC,②正确;由同底等高的三角形面积相等可得S△ABD= S△ADF,两边同时减去S△ADE可得S△ABE=S△DEF,③正确;根据△ABD面积的不同求法可求出AE=4.8,④错误,问题得解.
解:在长方形ABCD中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB(SSS),故①正确;
∵AF⊥BD,
∴在Rt△BEF中,∠BFE+∠FBE=90°,
∵在Rt△ACD中,∠CBD+∠BDC=90°,
∴∠BFE=∠BDC,故②正确;
∵S△ABD=![]() ,S△ADF=
,S△ADF=![]() ,
,
∴S△ABD= S△ADF,
∴S△ABD-S△ADE = S△ADF-S△ADE,即S△ABE=S△DEF,故③正确;
∵AB=6,AD=8,DB=10,
∴S△ABD=![]() ,
,
∴![]() ,故④错误,
,故④错误,
故选:C.

练习册系列答案
相关题目