题目内容
已知:点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M、N分别是射线AE、AF上的点,且PM=PN.
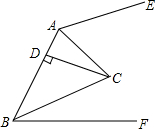
(1)当点M在线段AB上,点N在线段AC的延长线上时(如图1),求证:BM=CN;
(2)在(1)的条件下,AM+AN=______AC;
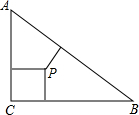
(3)当点M在线段AB的延长线上时(如图2),若AC:PC=2:1,PC=4,求四边形ANPM的面积.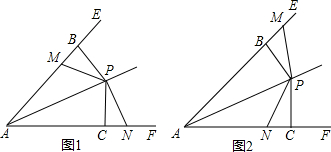
(1)当点M在线段AB上,点N在线段AC的延长线上时(如图1),求证:BM=CN;
(2)在(1)的条件下,AM+AN=______AC;
(3)当点M在线段AB的延长线上时(如图2),若AC:PC=2:1,PC=4,求四边形ANPM的面积.

(1)∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°,
在Rt△PBM和Rt△PCN中,
,
∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN;
(2)∵∠APB=90°-∠PAB,∠APC=90°-∠PAC,
∴∠APC=∠APB,
∵PB⊥AE,PC⊥AF,
∴PB=PC,
∴AM+AN=AM+CN+AC=AM+BM+AC=AB+AC=2AC;
故答案为:2;
(3)∵AC:PC=2:1,PC=4,
∴AC=8,
∴AB=AC=8,PB=PC=4,
∴S四边形ANPM=S△APN+S△APB+S△PBM=S△APN+S△APB+S△PCN=S△APC+S△APB=
AC•PC+
AB•PB=
×8×4+
×8×4=32.
∴PB=PC,∠PBM=∠PCN=90°,
在Rt△PBM和Rt△PCN中,
|
∴Rt△PBM≌Rt△PCN(HL),
∴BM=CN;
(2)∵∠APB=90°-∠PAB,∠APC=90°-∠PAC,
∴∠APC=∠APB,
∵PB⊥AE,PC⊥AF,
∴PB=PC,
∴AM+AN=AM+CN+AC=AM+BM+AC=AB+AC=2AC;
故答案为:2;
(3)∵AC:PC=2:1,PC=4,
∴AC=8,
∴AB=AC=8,PB=PC=4,
∴S四边形ANPM=S△APN+S△APB+S△PBM=S△APN+S△APB+S△PCN=S△APC+S△APB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目