题目内容
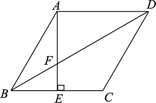
菱形ABCD中, AE⊥BC于E, 交BD于F点, 下列结论:
①BF为∠ABE的角平分线; ②DF=2BF;
③2AB2=DF·DB; ④sin∠BAE=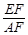 .
.
其中正确的为 ( )
A. ②③ B. ①②④ C. ①③④ C. ①④
①BF为∠ABE的角平分线; ②DF=2BF;
③2AB2=DF·DB; ④sin∠BAE=
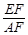 .
.
其中正确的为 ( )
A. ②③ B. ①②④ C. ①③④ C. ①④
C
解:①∵四边形ABCD是菱形,
∴BF为∠ABE的角平分线,
故①正确;
②连接AC交BD于点O,
∵四边形ABCD是菱形,
∴AB=BC=AD,
∴当∠ABC=60°时,△ABC是等边三角形,
即AB=AC,
则DF=2BF,
∵∠ABC的度数不定,
∴DF不一定等于2BF;
故②错误;
③∵AE⊥BC,AD∥BC,
∴AE⊥AD,
∴∠FAD=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD= DB,AD=AB,
DB,AD=AB,
∴∠AOD=∠FAD=90°,
∵∠ADO=∠FDO,
∴△AOD∽△FAD,
∴AD:DF=OD:AD,
∴AD2=DF?OD,
∴AB2=DF? DB,
DB,
即2AB2=DF?DB;
故③正确;
④连接CF,
在△ABF和△CBF中,
,
∴△ABF≌△CBF(SAS),
∴∠BCF=∠BAE,AF=CF,
在Rt△EFC中,sin∠ECF=
 =
= ,
,
∴sin∠BAE= .
.
故④正确.
故选C.
∴BF为∠ABE的角平分线,
故①正确;
②连接AC交BD于点O,
∵四边形ABCD是菱形,
∴AB=BC=AD,
∴当∠ABC=60°时,△ABC是等边三角形,
即AB=AC,

则DF=2BF,
∵∠ABC的度数不定,
∴DF不一定等于2BF;
故②错误;
③∵AE⊥BC,AD∥BC,
∴AE⊥AD,
∴∠FAD=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD=
 DB,AD=AB,
DB,AD=AB,∴∠AOD=∠FAD=90°,
∵∠ADO=∠FDO,
∴△AOD∽△FAD,
∴AD:DF=OD:AD,
∴AD2=DF?OD,
∴AB2=DF?
 DB,
DB,即2AB2=DF?DB;
故③正确;
④连接CF,
在△ABF和△CBF中,
|
∴△ABF≌△CBF(SAS),
∴∠BCF=∠BAE,AF=CF,
在Rt△EFC中,sin∠ECF=
 =
= ,
,∴sin∠BAE=
 .
.故④正确.
故选C.

练习册系列答案
相关题目
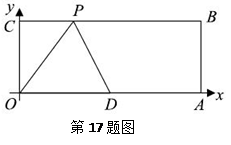











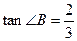 .求BC的长.
.求BC的长.