Question

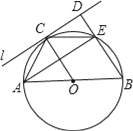
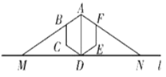
【题目】如图，过正六边形的顶点作一条直线于点，分别延长交直线于点，则___；若正六边形的面积为，则的面积为__．

Answer 1

【答案】

【解析】

因为正六边形每个内角都是120，AD⊥MN，且平分∠BAF，在直角三角形AMD中即可求得∠AMN=30；作出辅助线，利用特殊角以及三角形全等，可证得=8，同理可得：=8，最终即可求得=+=8+8=16．

如图，连接BECF相交于O，延长DC交AM于P，延长DE交AN于Q，

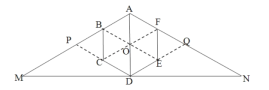
∵正六边形ABCDEF，

∴∠BAF=∠ABC=∠BCD=120，

∵AD是正六边形ABCDEF的对角线，

∴∠BAD=∠BAF=60，

∵AD⊥MN，∠ADM=90，

∴∠AMN=30

∴==，

∴∠PBC=∠PCB=60，

∴△PBC是等边三角形，

∴PB=PC=BC，

∵正六边形ABCDEF，

∴△ABO是等边三角形，AB=BC，

∴AB=OB=OA，

∴AB=OA=OB=BC=PB=PC，

∴△ABO△BCP(SSS) ，

∴==1，

∴=4，

在Rt△ADM中，∠AMD=30，

∴AM=2AD=4AB=2AP，

∴=8，

同理可得：=8，

∴=+=8+8=16．

故答案为：30，16．