题目内容
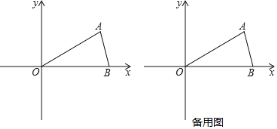
【题目】如图,已知正比例函数![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() .
.
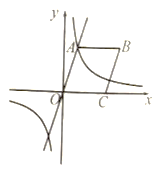
(1)填空:![]() 的值为_______________,
的值为_______________,![]() 的值为_____________;
的值为_____________;
(2)以点![]() 为圆心、
为圆心、![]() 为半径画弧交
为半径画弧交![]() 轴的正半轴于点
轴的正半轴于点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)观察上述反比例函数![]() 的图象,当
的图象,当![]() 时,请直接写出自变量
时,请直接写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据点![]() (1,
(1,![]() )在正比例函数
)在正比例函数![]() 与反比例函数
与反比例函数![]() 的图象上,将点A代入函数解析式求解即可;
的图象上,将点A代入函数解析式求解即可;
(2)根据题干作图方法和平行线性质,判断四边形OABC是菱形,再利用勾股定理进行计算即可求解;
(3)根据反比例函数图像性质求解即可.
解:(1)∵点A(1,a)为![]() 与
与![]() 的交点,
的交点,
∴将点A(1,a)代入![]() ,得
,得![]() ,
,
∴点A(1,3),
再将点A(1,3)代入![]() ,得
,得![]() ,
,
故答案为:![]() ,
,![]() ;
;
(2)如图,延长BA交y轴于点E,
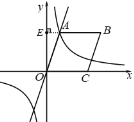
∵AB∥OC,
∴BE⊥y轴,
∴OE=3,AE=1,
由题意可知,OA=OC,
∴四边形OABC是菱形,
∴AB=OA=![]() ,
,
∴BE=![]() ,
,
∴点B的坐标为(![]() ,3);
,3);
(3)当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∵在第三象限图像中,y随x的增大而减小,
∴当![]() 时,
时,![]() ,
,
∵在第一象限的图像中,![]() 时,
时,![]() ,
,
综上:当![]() 时,x的取值范围为:
时,x的取值范围为:![]() 或
或![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目