题目内容
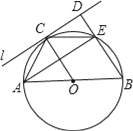
【题目】如图,![]() 的直径
的直径![]() ,
,![]() 为圆周上一点,
为圆周上一点,![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,过点
,过点![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求![]() 的度数;
的度数;
(2)求证:四边形![]() 是菱形.
是菱形.
【答案】(1)![]() =30°;(2)证明见解析.
=30°;(2)证明见解析.
【解析】
(1)易得△AOC是等边三角形,则∠AOC=60°,根据圆周角定理得到∠AEC=30°;
(2)根据切线的性质得到OC⊥![]() ,则有OC∥BD,再根据直径所对的圆周角为直角得到∠AEB=90°,则∠EAB=30°,可证得AB∥CE,得到四边形OBEC为平行四边形,再由OB=OC,即可判断四边形OBEC是菱形.
,则有OC∥BD,再根据直径所对的圆周角为直角得到∠AEB=90°,则∠EAB=30°,可证得AB∥CE,得到四边形OBEC为平行四边形,再由OB=OC,即可判断四边形OBEC是菱形.
(1)在△AOC中,AC=3,
∵AO=OC=3,
∴△AOC是等边三角形,
∴∠AOC=60°,
∴∠AEC=30°;
(2)∵OC⊥![]() ,BD⊥
,BD⊥![]() ,
,
∴OC∥BD,
∴∠ABD=∠AOC=60°,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴△AEB为直角三角形,∠EAB=30°.
∴∠EAB=∠AEC,
∴CE∥OB,
又∵CO∥EB,
∴四边形OBEC为平行四边形.
又∵OB=OC=3.
∴四边形OBEC是菱形.

练习册系列答案
相关题目
【题目】某工厂以每千克200元的价格购进甲种原料360千克,用于生产A、B两种产品,生产1件A产品或1件B产品所需甲、乙两种原料的千克数如下表:
产品/原料 | A | B |
甲(千克) | 9 | 4 |
乙(千克) | 3 | 10 |
乙种原料的价格为每千克300元,A产品每件售价3000元,B产品每件售价4200元,现将甲种原料全部用完,设生产A产品x件,B产品m件,公司获得的总利润为y元.
(1)写出m与x的关系式;
(2)求y与x的关系式;
(3)若使用乙种原料不超过510千克,生产A种产品多少件时,公司获利最大?最大利润为多少?