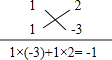Question

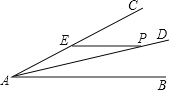
【题目】如图，点P是∠BAC的平分线AD上一点，且∠BAC=30°，PE∥AB交AC于点E，已知AE=2，则点P到AB的距离是（ ）

A.1.5B.C.1D.2

Answer 1

【答案】C

【解析】

过P作PF⊥AC于F，PM⊥AB于M，根据角平分线性质求出PF＝PM，根据平行线性质和等腰三角形的判定推出AE＝PE＝2，根据含30度角的直角三角形性质求出PF即可．

解：过点P作PF⊥AC于F，PM⊥AB于M，即PM是点P到AB的距离，

∵AD是∠BAC的平分线，PF⊥AC，PM⊥AB，

∴PF＝PM，∠EAP＝∠PAM，

∵PE∥AB，

∴∠EPA＝∠PAM，

∴∠EAP＝∠EPA，

∵AE＝2，

∴PE＝AE＝2，

∵∠BAC＝30°，PE∥AB，

∴∠FEP＝∠BAC＝30°，

∵∠EFP＝90°，

∴PF＝PE＝1，

∴PM＝PF＝1，

故选：C．