��Ŀ����
����Ŀ���Ķ���˼������ʽ�˷�����ʽ�ֽ��Ƿ����෴�ı��Σ��ɣ�x+p����x+q��=x2+��p+q��x+pq�ã�x2+��p+q��x+pq=��x+p����x+q�����������ʽ�ӿ��Խ�ijЩ������ϵ����1�Ķ�������ʽ�ֽ���ʽ�����磺��ʽ��x2��x��6�ֽ���ʽ�����ʽ�ӵij����6=2������3����һ����ϵ����1=2+����3����������̿���ʮ����˵���ʽ����ر�ʾ���ȷֽⳣ����ֱ�д��ʮ�ֽ����ߵ����ϽǺ����½ǣ��ٷֽⳣ����ֱ�д��ʮ�ֽ����ߵ����ϽǺ����½ǣ�Ȼ����ˣ�������ͣ�ʹ�����һ����ϵ������ͼ��ʾ�����ַֽ��������ʽ�ķ����С�ʮ����˷�������ͬѧ������۲죬�����������������⣮
��1���ֽ���ʽ��x2+7x��18��
��2����գ���x2+px��8�ɷֽ�Ϊ����һ����ʽ�Ļ���������p�����п���ֵ�� ��
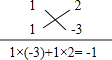
���𰸡���1����x+9����x��2������2��7����7��2����2
��������
�����������1����������ʮ����˷���ԭʽ�ֽ⼴�ɣ�
��2���ѩ�8��Ϊ����������ˣ���ͼ�Ϊ����p��ֵ��д�����ɣ�
�⣺��1��ԭʽ=��x+9����x��2����
��2����x2+px��8�ɷֽ�Ϊ����һ����ʽ�Ļ���������p�����п���ֵ�ǩ�8+1=��7����1+8=7����2+4=2����4+2=��2��
�ʴ�Ϊ��7����7��2����2

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�