题目内容
【题目】新华中学暑假要进行全面维修，有甲、乙两个工程队共同完成，甲队单独完成这项工程所需天数是乙队单独完成所需天数的
，若由甲队先做10天，剩下的工程再由甲、乙两队合作，再做30天可以完成．
(1)求甲、乙两队单独完成这项工程各需多少秀？
(2)已知甲队每天的施工费用为0.84万元，乙队每天的施工费用为0.56万元，若由甲、乙两队合作，则工程预算的施工费用50万元是否够用?若不够用，需追加多少万元?
【答案】（1）甲乙两队单独完成这項工程雷要60天和90天；（2）工程預算费用不够，需追要0.4万元．
【解析】
（1）由题意设乙队单独完成这项工程需要
天，则甲队单独完戒这项工程需要
天，根据题意列出方程求解即可；
（2）由题意设甲乙两队合作完成这项工程需要
天，并根据题意解出y的值，进而进行分析即可.
解：(1)设乙队单独完成这项工程需要天，则甲队单独完戒这项工程需要天，依题意则有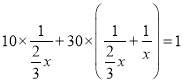
解得
经检验，是原分式方程的解，且符合题意
(天)
故甲乙两队单独完成这項工程雷要60天和90天．
（2)设甲乙两队合作完成这项工程需要天，
则
解得y=36
所需费用
(万元)
，
∴工程預算费用不够，需追要0.4万元．
练习册系列答案
相关题目
