题目内容
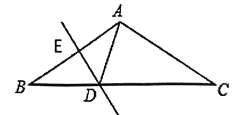
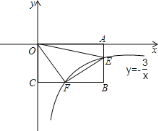
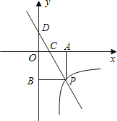
【题目】如图，一次函数
的图象分别交
轴、
轴于点
、点
，与反比例函数
的图象在第四象限的相交于点
，并且
轴于点
，
轴于点
，已知
，且
求上述一次函数与反比例函数的表达式；
求一次函数与反比例函数的另一个交点坐标．
【答案】(1)
,(2)
.
【解析】
（1）令一次函数解析式中x=0，求出对应的y值，确定出D的坐标，得到OD的长，再由B的坐标得到OB的长，由OD+OB求出BD的长，在直角三角形BDP中，利用两直角边乘积的一半表示出三角形的面积，将BD及已知的面积代入求出BP的长，确定出P的坐标，由P为一次函数与反比例函数的交点，将P的坐标代入一次函数解析式中求出k的值，确定出一次函数解析式，将P的坐标代入反比例函数解析式中求出m的值，确定出反比例函数解析式；（2）将一次函数解析式与反比例函数解析式联立组成方程组，求出方程组的解即可得到两函数的另一个交点．
解：
令一次函数解析式
中
，解得
，
∴
坐标为
，即
，
又
，即
，
∴
，
∵
，
∴
，
∴
的坐标为
，
将
，
代入一次函数解析式得：
，
解得：
，
∴一次函数解析式为
，
将，代入反比例解析式得：
，
解得：
，
∴反比例函数的表达式为
；
联立两个关系式得：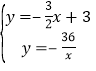
，
消去
得：
，
整理得：
，
解得：
，
，
经检验是原方程的解，
∴
，
，
∴一次函数与反比例函数交点为或，
则一次函数与反比例函数的另一交点坐标为．
练习册系列答案
相关题目
