题目内容
【题目】(13分)如图所示,四边形![]() 中,
中, ![]() 于点
于点![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点。
上的一个动点。
(1)求证: ![]() 。
。
(2)过点![]() 分别作
分别作![]() 于
于![]() 点,作
点,作![]() 于
于![]() 点。
点。
① 试说明![]() 为定值。
为定值。
② 连结![]() ,试探索:在点
,试探索:在点![]() 运动过程中,是否存在点
运动过程中,是否存在点![]() ,使
,使![]() 的值最小。若存在,请求出该最小值;若不存在,请说明理由。
的值最小。若存在,请求出该最小值;若不存在,请说明理由。
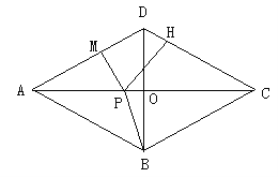
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:(1)由AC⊥BD,AO=CO,可知BD是AC的垂直平分线,由线段垂直平分线的性质可知AD=DC,AB=BC,同理可得AD=AB,CD=BC,故AB=BC=CD=AD;或先根据对角线互相平分的四边形是平行四边形先证四边形ABCD是平行四边形,然后根据对角线互相垂直的平行四边形是菱形证明四边形ABCD是菱形,进而得出结论;
(2)连接DP,根据题意可知: S△ADC=S△ADP+S△CDP,由三角形的面积公式可知: ![]() ACOD =
ACOD =![]() ADPM+
ADPM+![]() DCPH,将AC、OD、AD、DC的长代入化简即可;
DCPH,将AC、OD、AD、DC的长代入化简即可;
(3))由PM+PH为定值,当PB最短时,PM+PH+PB有最小值,由垂线的性质可知当点P与点O重合时,OB有最小值.
试题解析:
(1)证明:∵AO=CO,BD⊥AC,
∴AD=CD,AB=BC ,
同理可得AD=AB,CD=BC,
∴AB=BC=CD=AD;
另证:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形,
∴AB=BC=CD=AD.
(2)证明:∵AC⊥BD,BO=DO=5,AO=CO=12,
∴由勾股定理得AD=CD=13,
连结DP则S△ADC=S△ADP+S△CDP ,
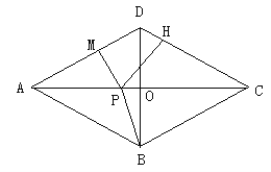
又∵PM⊥AD,PH⊥DC,DO⊥AC,
∴![]()
∴![]()
∴![]() 即
即![]() 为定值;
为定值;
(3)存在点![]() ,使
,使![]() 的值最小.
的值最小.
由(2)可知, ![]() 为定值
为定值
∴要使PM+PH+PB最小,则PB要取最小值
∵BO⊥AC,
∴当P与O重合时,PB最小,最小值为OB=5,
∴PM+PH+PB的最小值为![]() .
.