��Ŀ����
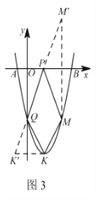
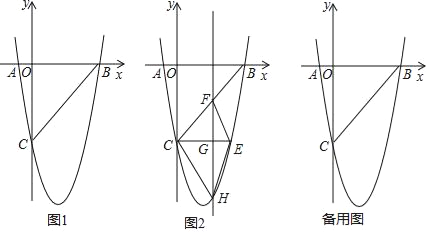
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪������y=ax2+bx��5��x�ύ��A����1��0����B��5��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
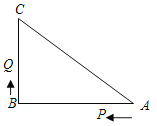
��2����ͼ2��CE��x�����������ཻ�ڵ�E����H��ֱ��CE�·��������ϵĶ��㣬����H����y��ƽ�е�ֱ����BC��CE�ֱ��ཻ�ڵ�F��G����̽������H�˶����δ�ʱ���ı���CHEF�����������H�����ꣻ
��3������KΪ�����ߵĶ��㣬��M��4��m���Ǹ��������ϵ�һ�㣬��x�ᣬy���Ϸֱ��ҵ�P��Q��ʹ�ı���PQKM���ܳ���С�������P��Q�����꣮
���𰸡���1��y=x2��4x��5��2����![]() ����
����![]() ������3��P��
������3��P��![]() ��0����Q��0����
��0����Q��0����![]() ��
��
�����������������
��1���ô���ϵ�����������ߵĽ���ʽ����2����H(t��t2-4t-5)���ú�t�Ĵ���ʽ��ʾFH�ij������CE�ij����öԽ����ഹֱ���ı��ε�������ڶԽ�����һ�룬���ı���CHEF�������ʾΪ����t�Ķ��κ������ö��κ�����������⣻��3������M��K����x�ᣬy��ԳƵ�M�䣬K��������M��K�䣬�ֱ�x����y���ڵ�P��Q�����M��K���Ľ���ʽ�����ɵõ���P��Q������.
������1����A(-1��0)��B(5��0)����y=ax2+bx-5��
![]() �����
�����![]()
����κ����ı���ʽΪy=x2-4x-5
��2����ͼ2����H(t��t2-4t-5)��
��CE||x�ᣬ��-5=x2-4x-5����ã�x1=0��x2=4��
��E(4��-5)����CE=4��
��B(5��0)��C(0��-5)��
![]() ��
��![]() ��
��
��ֱ��BC�Ľ���ʽΪy2=x-5����F(t��t-5)��
��CE||x�ᣬHF||y�ᣬ��CE��HF��
���ı���CHEF�����=![]() )2+
)2+![]() ��
��
��H(![]() .
.
��3����ͼ3��
�ߵ�KΪ���㣬��K(2��-9)��
���K����y��ĶԳƵ�K��������Ϊ(-2��-9)��
��M(4��m)����M(4��-5)��
���M����x��ĶԳƵ�M��������Ϊ(4��5)��
��ֱ��K��M���Ľ���ʽΪy3=a3x+b3��
![]() ����
����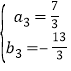
��ֱ��BC�Ľ���ʽΪy3=![]() ��
��
��P��Q������ֱ�ΪP(![]() ��0)��Q(0��-
��0)��Q(0��-![]() .
.