题目内容
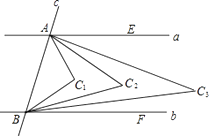
【题目】在△ABC中,∠ACB=90°,∠A<45°,点O为AB中点,一个足够大的三角板的直角顶点与点O重合,一边OE经过点C,另一边OD与AC交于点M.
(1)如图1,当∠A=30°时,求证:MC2=AM2+BC2;
(2)如图2,当∠A≠30°时,(1)中的结论是否成立?如果成立,请说明理由;如果不成立,请写出你认为正确的结论,并说明理由;
(3)将三角形ODE绕点O旋转,若直线OD与直线AC相交于点M,直线OE与直线BC相交于点N,连接MN,则MN2=AM2+BN2成立吗?答: (填“成立”或“不成立”)

【答案】(1)、证明过程见解析;(2)、理由见解析;(3)、成立.
【解析】
试题分析:(1)、根据点O为中点,∠ACB=90°得出OA=OB=OC,根据∠A=30°可得∠B=∠COB=60°,根据∠COM=90°得出∠AOM=∠A=30°,则AM=OM,根据Rt△COM的勾股定理得出所求的答案;(2)、过A作AF‖BC交CO的延长线于点F,连接FM,证明△BOC≌△AOF,得出BC=AF,FO=CO,根据Rt△AMF的勾股定理进行说明.
试题解析:(1)、∵O为AB中点,∠ACB=90°∴OA=OB=OC,∵∠A=30°∴∠B=60°
∴∠COB=60° ∵∠COM=90°∴∠AOM=∠A=30°∴AM=OM
在Rt△COM中,由勾股定理得MC2=OM2+OC2∴ MC2=AM2+BC2;
(2)、成立。如图,
 过A作AF‖BC交CO的延长线于点F,连接FM
过A作AF‖BC交CO的延长线于点F,连接FM
∵O为AB中点,可证△BOC≌△AOF,∴BC=AF,FO=CO ∵AF‖BC,∠ACB=90°∴∠CAF=90°
∵FO=CO,∠MOC=90°,∴OM是CF的垂直平分线,∴CM=MF,
在Rt△AMF中,由勾股定理得:MF2=AM2+AF2=AM2+BC2, 即MC2=AM2+BC2
(3)、成立。

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案