题目内容
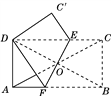
【题目】如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.

(1)求证:EG=CH;
(2)已知AF=![]() ,求AD和AB的长.
,求AD和AB的长.
【答案】(1)见解析(2)AD= ![]() +2;AB= 2
+2;AB= 2![]() +2.
+2.
【解析】
试题分析:(1)由折叠的性质及矩形的性质可知AE=AD=EG,BC=CH,再根据四边形ABCD是矩形,可得AD=BC,等量代换即可证明EG=CH;
(2)由折叠的性质可知∠ADE=45°,∠FGE=∠A=90°,AF=![]() ,那么DG=
,那么DG=![]() ,利用勾股定理求出DF=2,于是可得AD=AF+DF=
,利用勾股定理求出DF=2,于是可得AD=AF+DF=![]() +2;再利用AAS证明△AEF≌△BCE,得到AF=BE,于是AB=AE+BE=
+2;再利用AAS证明△AEF≌△BCE,得到AF=BE,于是AB=AE+BE=![]() +2+
+2+![]() =2
=2![]() +2.
+2.
试题解析:(1)证明:由折叠知AE=AD=EG,BC=CH,
∵四边形ABCD是矩形,
∴AD=BC,
∴EG=CH;
(2)解:∵∠ADE=45°,∠FGE=∠A=90°,AF=![]() ,
,
∴DG=![]() ,DF=2,
,DF=2,
∴AD=AF+DF=![]() +2;
+2;
由折叠知∠AEF=∠GEF,∠BEC=∠HEC,
∴∠GEF+∠HEC=90°,∠AEF+∠BEC=90°,
∵∠AEF+∠AFE=90°,
∴∠BEC=∠AFE,
在△AEF与△BCE中,
 ,
,
∴△AEF≌△BCE(AAS),
∴AF=BE,
∴AB=AE+BE=![]() +2+
+2+![]() =2
=2![]() +2.
+2.

练习册系列答案
相关题目