��Ŀ����
����Ŀ�����Ķ����в��ϣ��������Ӧ������
÷����˹��Menelaus���ǹ�Ԫһ����ʱ��ϣ����ѧ�Ҽ�����ѧ�ң����м���ѧ������ѧ����������鼮��÷����˹���֣������θ��ߣ������ӳ��ߣ���һ�������κ�һ������Ҳ�����κ�һ����ƽ�е�ֱ�����أ�����ֱ�߿����������ε��������ཻ��һ��������һ���ߵ��ӳ����ཻ����Ҳ�����������߶����ཻ���������ߵ��ӳ��߶��ཻ�����������������о���֤����������÷����˹���������÷�϶�������
��D��E��F�����ǡ�ABC������AB��BC��CA�����ӳ����ϵĵ㣬�������㹲�ߣ�������![]() ��
��
���������֤���������£�
���������ͼ1��ֱ��DE����ABC�ı�AB�ڵ�D������AC�ڵ�F������BC���ӳ������E��
����C��CM��DE��AB�ڵ�M����![]() ��
��![]() �����ݣ���
�����ݣ���
��![]() ��
��![]() ��
��
��BEADFC��BDAFEC����![]() ��
��
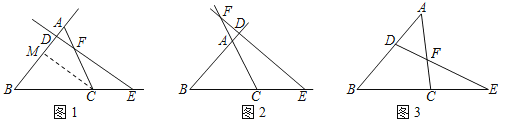
���������ͼ2��ֱ��DE�ֱ�ABC�ı�BA��BC��CA���ӳ����ڵ�D��E��F��
��
��1��������е�����ָ���� ����
��2����������������֤��˼·����������֤����
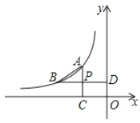
��3����ͼ3��D��F�ֱ��ǡ�ABC�ı�AB��AC�ϵĵ㣬��AD:DB��CF:FA��2:3������DF���ӳ�����BC���ӳ����ڵ�E����ôBE:CE���� ����
���𰸡���1������ֱ�߱�һ��ƽ�������أ����õĶ�Ӧ�߶γɱ�������2����������(3)![]()
��������
��1������ƽ���߷��߶γɱ�������������⼴�ɣ�
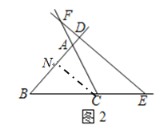
��2����ͼ2�У���CN��DE��BD��N��ģ������ٵķ���������⼴�ɣ�
��3������÷�϶���![]() ���ɽ�����⣮
���ɽ�����⣮
�⣺��1��������е������ǣ�����ֱ�߱�һ��ƽ�������أ����õĶ�Ӧ�߶γɱ�����
�ʴ�Ϊ������ֱ�߱�һ��ƽ�������أ����õĶ�Ӧ�߶γɱ�����
��2����ͼ2�У���CN��DE��BD��N��
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]()
![]() ��
��![]()
![]() ��
��
��BEADFC��BDAFEC��
��![]() ��1��
��1��
��3����![]()
![]() ��1��AD:DB��CF:FA��2:3��
��1��AD:DB��CF:FA��2:3��
��![]() ��1����
��1����![]() =
=![]() ��
��
�ʴ�Ϊ��![]() ��
��

����Ŀ��ijУ���꼶ѧ��С����Сǿ��С�쵽ij���вμ������ʵ������ڻ�����Dz�����ij��ˮ�������۹�������֪��ˮ���Ľ���Ϊ8Ԫ/ǧ�ˣ������������ڻ������ĶԻ���
С���������10Ԫ/ǧ�˵ļ۸����ۣ���ôÿ����۳�300ǧ�ˣ�
Сǿ�����ÿǧ�˵�����Ϊ3Ԫ����ôÿ����۳�250ǧ�ˣ�
С�죺�����13Ԫ/ǧ�˵ļ۸����ۣ���ôÿ��ɻ�ȡ����750Ԫ��
������=�����ۼ�-���ۣ�![]() ��������
��������
��1����������ǵĶԻ���д�±���
���۵���x��Ԫ/kg�� | 10 | 11 | 13 |
������y��kg�� |
��2��������ݱ����е���Ϣ�ж�ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮����������ĺ�����ϵ������y��ǧ�ˣ���x��Ԫ����x��0���ĺ�����ϵʽ��
��3����ó�����������ˮ��ÿ���ȡ������ΪWԪ����W��x�ĺ�����ϵʽ�������۵���Ϊ��ֵʱ��ÿ��ɻ�õ����������������Ƕ���Ԫ��