Question

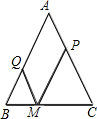
如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．
（1）求四边形AQMP的周长；
（2）写出图中的两对相似三角形（不需证明）；
（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．

Answer 1

（1）∵AB∥MP，QM∥AC，
∴四边形APMQ是平行四边形，∠B=∠PMC，∠C=∠QMB．
∵AB=AC，
∴∠B=∠C，
∴∠PMC=∠QMB．
∴BQ=QM，PM=PC．
∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=2a．

（2）∵PM∥AB，
∴△PCM∽△ACB，
∵QM∥AC，
∴△BMQ∽△BCA；

（3）当点M在BC的中点时，四边形APMQ是菱形，
∵AB∥MP，点M是BC的中点，
∴

CM

CB

=

CP

AC

=

1

2

，
∴P是AC的中点，
∴PM是三角形ABC的中位线，
同理：QM是三角形ABC的中位线．
∵AB=AC，
∴QM=PM=

1

2

AB=

1

2

AC．
又由（1）知四边形APMQ是平行四边形，
∴平行四边形APMQ是菱形．