题目内容
如图，BC是⊙O的直径，AB、AD是⊙O的切线，切点分别为B、P，过C点的切线与AD交于点D，连接AO、DO．
求证：△ABO∽△OCD．
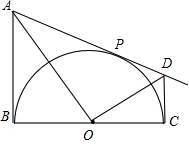
求证：△ABO∽△OCD．
证明：连接OP，
∵A点切线BA和AD的交点，D点为过C点的切线和切线AD的交点，
∴△ABO≌△APO，△COD≌△POD，
∴2∠DOP+2∠AOP=180°，
∴∠AOD=90°，
∴∠AOB+∠COD=90°，
∵∠AOB+∠OAB=90°，
∴∠OAB=∠DOC，
∵∠ABO=∠OCD=90°，
∴△ABO∽△OCD．
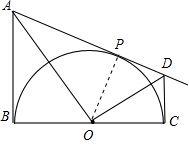
∵A点切线BA和AD的交点，D点为过C点的切线和切线AD的交点，
∴△ABO≌△APO，△COD≌△POD，
∴2∠DOP+2∠AOP=180°，
∴∠AOD=90°，
∴∠AOB+∠COD=90°，
∵∠AOB+∠OAB=90°，
∴∠OAB=∠DOC，
∵∠ABO=∠OCD=90°，
∴△ABO∽△OCD．
练习册系列答案
教材全解字词句篇系列答案
相关题目
