Question

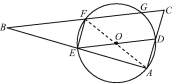
【题目】如图，已知ED为☉O的直径且ED=4，点A(不与点E，D重合)为☉O上一个动点，线段AB经过点E，且EA=EB，F为☉O上一点，∠FEB=90°，BF的延长线交AD的延长线于点C.

(1)求证:△EFB≌△ADE；

(2)当点A在☉O上移动时，直接回答四边形FCDE的最大面积为多少.

Answer 1

【答案】(1)证明见解析；(2)四边形FCDE的最大面积是8.

【解析】

（1）连接FA，根据垂直的定义得到EF⊥AB，得到BF=AF，推出BF=ED，根据全等三角形的判定定理即可得到结论；
（2）根据全等三角形的性质得到∠B=∠AED，得到DE∥BC，推出四边形形FCDE，得到E到BC的距离最大时，四边形FCDE的面积最大，即点A到DE的距离最大，推出当A为的中点时，于是得到结论．

(1)连接FA,

∵∠FEB=90°,

∴EF⊥AB,

∵BE=AE,

∴BF=AF,

∵∠FEA=∠FEB=90°,

∴AF是☉O的直径,

∴AF=DE,

∴BF=ED,

在Rt△EFB与Rt△ADE中,

∴Rt△EFB≌Rt△ADE.

(2)∵Rt△EFB≌Rt△ADE,

∴∠B=∠AED,

∴DE∥BC,

∵ED为☉O的直径,

AC⊥AB,

∵EF⊥AB,

∴EF∥CD,

∴四边形FCDE是平行四边形,

∴E到BC的距离最大时,四边形FCDE的面积最大,即点A到DE的距离最大,

∴当A为的中点时,点A到DE的距离最大是2,

∴四边形FCDE的最大面积=4×2=8.