题目内容
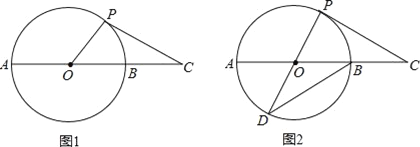
【题目】如图1,正方形ABCD的一边AB在直尺一边所在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E.

(1)如图1,线段AB与OE之间的数量关系为 .(请直接填结论)
(2)保证点A始终在直线MN上,正方形ABCD绕点A旋转θ(0<θ<90°),过点 B作BF⊥MN于点F.
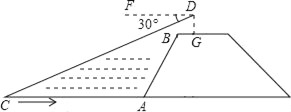
①如图2,当点O、B两点均在直线MN右侧时,试猜想线段AF、BF与OE之间存在怎样的数量关系?请说明理由.
②如图3,当点O、B两点分别在直线MN两侧时,此时①中结论是否依然成立呢?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.
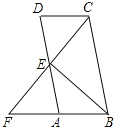
③当正方形ABCD绕点A旋转到如图4的位置时,线段AF、BF与OE之间的数量关系为 .(请直接填结论)
【答案】(1)AB=2OE;(2)①AF+BF=2OE,证明见解析;②AF﹣BF=2OE 证明见解析;③BF﹣AF=2OE,
【解析】试题分析:(1)利用直角三角形斜边的中线等于斜边的一半即可得出结论;
(2)①过点B作BH⊥OE于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBH,然后利用“角角边”证明△AOE和△OBH全等,根据全等三角形对应边相等可得OH=AE,OE=BH,再根据AF-EF=AE,整理即可得证;
②过点B作BH⊥OE交OE的延长线于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBH,然后利用“角角边”证明△AOE和△OBH全等,根据全等三角形对应边相等可得OH=AE,OE=BH,再根据AF-EF=AE,整理即可得证;
③同②的方法可证.
试题解析:(1)∵AC,BD是正方形的对角线,
∴OA=OC=OB,∠BAD=∠ABC=90°,
∵OE⊥AB,
∴OE=![]() AB,
AB,
∴AB=2OE,
(2)①AF+BF=2OE
证明:如图2,过点B作BH⊥OE于点H
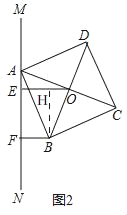
∴∠BHE=∠BHO=90°
∵OE⊥MN,BF⊥MN
∴∠BFE=∠OEF=90°
∴四边形EFBH为矩形
∴BF=EH,EF=BH
∵四边形ABCD为正方形
∴OA=OB,∠AOB=90°
∴∠AOE+∠HOB=∠OBH+∠HOB=90°
∴∠AOE=∠OBH
∴△AEO≌△OHB(AAS)
∴AE=OH,OE=BH
∴AF+BF=AE+EF+BF=OH+BH+EH=OE+OE=2OE.
②AF﹣BF=2OE
证明:如图3,延长OE,过点B作BH⊥OE于点H
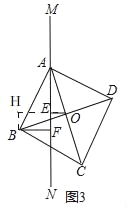
∴∠EHB=90°
∵OE⊥MN,BF⊥MN
∴∠AEO=∠HEF=∠BFE=90°
∴四边形HBFE为矩形
∴BF=HE,EF=BH
∵四边形ABCD是正方形
∴OA=OB,∠AOB=90°
∴∠AOE+∠BOH=∠OBH+∠BOH
∴∠AOE=∠OBH
∴△AOE≌△OBH(AAS)
∴AE=OH,OE=BH,
∴AF﹣BF
=AE+EF﹣HE=OH﹣HE+OE=OE+OE=2OE
③BF﹣AF=2OE,
如图4,作OG⊥BF于G,则四边形EFGO是矩形,
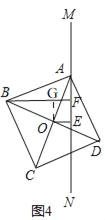
∴EF=GO,GF=EO,∠GOE=90°,
∴∠AOE+∠AOG=90°.
在正方形ABCD中,OA=OB,∠AOB=90°,
∴∠AOG+∠BOG=90°,
∴∠AOE=∠BOG.
∵OG⊥BF,OE⊥AE,
∴∠AEO=∠BGO=90°.
∴△AOE≌△BOG(AAS),
∴OE=OG,AE=BG,
∵AE﹣EF=AF,EF=OG=OE,AE=BG=AF+EF=OE+AF,
∴BF﹣AF=BG+GF﹣(AE﹣EF)=AE+OE﹣AE+EF=OE+OE=2OE,
∴BF﹣AF=2OE.

【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.