题目内容
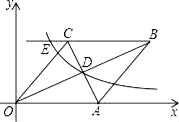
【题目】如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D，连接BD、BE、CE，若∠CBD=32°，则∠BEC的度数为________．
【答案】122°
【解析】在O中,∵∠CBD=32°，
∵∠CAD=32°，
∵点E是△ABC的内心，
∴∠BAC=64°，
∴∠EBC+∠ECB=(180°64°)÷2=58°，
∴∠BEC=180°58°=122°.
故答案为：122°.
点睛: 本题考查了三角形的内心，三角形的外接圆，圆周角定理，三角形内角和定理，三角形外角性质．熟知三角形的内心（三角形的三条角平分线交于一点，该点即为三角形的内心）和根据圆周角定理得出角的数量关系是解题的关键.内心是三角形角平分线交点的原理：经圆外一点作圆的两条切线，这一点与圆心的连线平分两条切线的夹角（原理：角平分线上点到角两边距离相等）。内心定理：三角形的三个内角的角平分线交于一点。该点叫做三角形的内心.
练习册系列答案
优质课堂快乐成长系列答案
相关题目
