题目内容
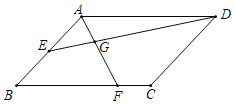
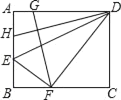
【题目】如图,将矩形ABCD沿DE折叠,点A恰好落在BC上的点F处,点G、H分别在AD、AB上,且FG⊥DH,若tan∠ADE=![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
利用翻折变换的性质得出△EBF∽△FCD,进而求出![]() 的值,再利用已知得出得△GNF∽△DAH,则
的值,再利用已知得出得△GNF∽△DAH,则![]() .
.
∵将矩形ABCD沿DE折叠,点A恰好落在BC上的点F处,
∴AE=EF,∠EFD=90°,
∴∠EFB+∠DFC=90°,
∵∠DFC+∠CDF=90°,
∴∠CDF=∠EFB,
又∵∠B=∠C,
∴△EBF∽△FCD,
∴![]() ,
,
∵tan∠ADE=![]() ,
,
∴tan∠EDF=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴设BE=a,BF=x,则FC=2a,DC=2x,
故EF+BE=DC,
则![]() +a=2x,
+a=2x,
整理得:a=![]() x,
x,
故![]() =
= =
=![]() ,
,
过点G作GN⊥BC于点N,
∴四边形ABNG是矩形,
∴AB=GN=DC,∠GNF=∠NGD=90°,
∴∠NGF+∠FGD=90°,
∵FG⊥DH,四边形ABCD是矩形,
∴AD=BC,∠FGD+∠GDM=90°,∠GNF=∠A,
∴∠GDM=∠NGF,
∴△GNF∽△DAH,
∴![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
故选:B.


练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目