题目内容
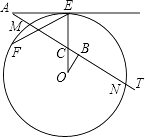
【题目】如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3 ![]() ,MN=2
,MN=2 ![]() .
. 
(1)求∠COB的度数;
(2)求⊙O的半径R;
(3)点F在⊙O上( ![]() 是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
【答案】
(1)解:∵AE切⊙O于点E,
∴AE⊥CE,又OB⊥AT,
∴∠AEC=∠CBO=90°,
又∠BCO=∠ACE,
∴△AEC∽△OBC,又∠A=30°,
∴∠COB=∠A=30°
(2)解:∵AE=3 ![]() ,∠A=30°,
,∠A=30°,
∴在Rt△AEC中,tanA=tan30°= ![]() ,即EC=AEtan30°=3,
,即EC=AEtan30°=3,
∵OB⊥MN,∴B为MN的中点,又MN=2 ![]() ,
,
∴MB= ![]() MN=
MN= ![]() ,
,
连接OM,在△MOB中,OM=R,MB= ![]() ,
,
∴OB= ![]() ,
,
在△COB中,∠BOC=30°,
∵cos∠BOC=cos30°= ![]() ,
,
∴BO= ![]() OC,
OC,
∴OC= ![]() OB=
OB= ![]()
![]() ,
,
又OC+EC=OM=R,
∴R= ![]()
![]() +3,
+3,
整理得:R2+18R﹣115=0,即(R+23)(R﹣5)=0,
解得:R=﹣23(舍去)或R=5,
则R=5
(3)解:以EF为斜边,有两种情况,以EF为直角边,有四种情况,所以六种,
画直径FG,连接EG,延长EO与圆交于点D,连接DF,如图所示:
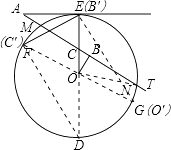
∵EF=5,直径ED=10,可得出∠FDE=30°,
∴FD=5 ![]() ,
,
则C△EFD=5+10+5 ![]() =15+5
=15+5 ![]() ,
,
由(2)可得C△COB=3+ ![]() ,
,
∴C△EFD:C△COB=(15+5 ![]() ):(3+
):(3+ ![]() )=5:1.
)=5:1.
∵EF=5,直径FG=10,可得出∠FGE=30°,
∴EG=5 ![]() ,
,
则C△EFG=5+10+5 ![]() =15+5
=15+5 ![]() ,
,
∴C△EFG:C△COB=(15+5 ![]() ):(3+
):(3+ ![]() )=5:1
)=5:1
【解析】(1)由AE与圆O相切,根据切线的性质得到AE与CE垂直,又OB与AT垂直,可得出两直角相等,再由一对对顶角相等,利用两对对应角相等的两三角形相似可得出三角形AEC与三角形OBC相似,根据相似三角形的对应角相等可得出所求的角与∠A相等,由∠A的度数即可求出所求角的度数;(2)在直角三角形AEC中,由AE及tanA的值,利用锐角三角函数定义求出CE的长,再由OB垂直于MN,由垂径定理得到B为MN的中点,根据MN的长求出MB的长,在直角三角形OBM中,由半径OM=R,及MB的长,利用勾股定理表示出OB的长,在直角三角形OBC中,由表示出OB及cos30°的值,利用锐角三角函数定义表示出OC,用OE﹣OC=EC列出关于R的方程,求出方程的解得到半径R的值;(3)把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合,在EF的同一侧,这样的三角形共有3个.延长EO与圆交于点D,连接DF,如图所示,由第二问求出半径,的长直径ED的长,根据ED为直径,利用直径所对的圆周角为直角,得到三角形EFD为直角三角形,由∠FDE为30°,利用锐角三角函数定义求出DF的长,表示出三角形EFD的周长,再由第二问求出的三角形OBC的三边表示出三角形BOC的周长,即可求出两三角形的周长之比.

 阅读快车系列答案
阅读快车系列答案