题目内容
【题目】已知：直线y=﹣x﹣4分别交x、y轴于A、C两点，抛物线y=ax2+bx（a＞0）经过A、O两点，且顶点B的纵坐标为﹣2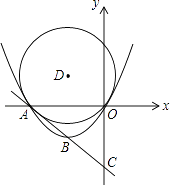 
（1）判断点B是否在直线AC上，并求该抛物线的函数关系式；
（2）以点B关于x轴的对称点D为圆心，以OD为半径作⊙D，试判断直线AC与⊙D的位置关系，并说明理由；
（3）若E为⊙D的优弧AO上一动点（不与A、O重合），连结AE、OE，问在抛物线上是否存在点P，使∠POA：∠AEO=2：3？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．
【答案】
（1）解：∵点A、C分别是直线y=﹣x﹣4与x、y轴的交点，
∴点A（﹣4，0），点C（0，﹣4），
由题意可得： 
，
解得 
，
∴抛物线的函数关系式为y= 
x2+2x．
由y= x2+2x= （x+2）2﹣2得顶点B（﹣2，﹣2）．
当x=﹣2时，y=﹣x﹣4=﹣2，
∴点B在直线y=﹣x﹣4上
（2）解：直线AC与⊙D相切．
理由：连接DA，如图1．
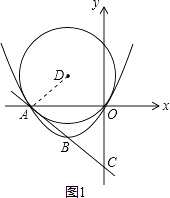
∵A（﹣4，0），C（0，﹣4），
∴OA=OC=4．
∵∠AOC=90°，
∴∠OAC=∠OCA=45°．
∵点B在直线AC上，
∴∠BAO=45°．
∵点B与点D关于x轴对称，
∴∠DAO=∠BAO=45°，
∴∠DAB=90°，
∵抛物线y=ax2+bx（a＞0）经过A、O两点，顶点是B，点B与点D关于x轴对称，OD为半径，
∴直线AC与⊙D相切
（3）解：过点P作PH⊥x轴于H，如图2①、图2②，
∵DA=DO，
∴∠DOA=∠DAO=45°，
∴∠ADO=90°．
∵E为⊙D的优弧AO上一动点（不与A、O重合），
∴∠AEO= ∠ADO=45°．
∵∠POA：∠AEO=2：3，
∴∠POA= 
∠AEO= ×45°=30°．
∴直线OP的解析式为y= 
x，或y=﹣ x．
①当直线OP的解析式为y=﹣ x时，如图2①，
解方程组 
，得
或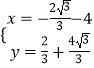 
，
∴点P的坐标为（﹣ 
﹣4， + 
）．
②当直线OP的解析式为y= x时，如图2②，
解方程组 ，得
或 ，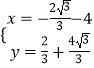
∴点P的坐标为（ 
， 
）．
综上所述：点P的坐标为（﹣ ﹣4 
）或（ -4， ）．
【解析】（1）可先求出点A、C的坐标，然后结合点A的坐标及顶点B的纵坐标为﹣2可得到关于a、b的方程组，然后解这个方程组，就可得到抛物线的函数关系式，从而得到点B的坐标，然后把点B的坐标代入直线AC的解析式，就可解决问题；（2）连接DA，如图1，要证直线AC与⊙D相切，只需证∠DAC=90°；（3）过点P作PH⊥x轴于H，如图2①、图2②，易得∠ADO=90°，根据圆周角定理可得∠AEO，从而求出∠POA，从而可得到直线OP的解析式，然后解直线OP与抛物线的解析式组成的方程组，就可得到点P的坐标．
