题目内容
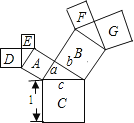
【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出了2个小正方形(如图①),其中,3个正方形围成的三角形是直角三角形.再经过一次“生长”后,又生出了4个小正方形(如图②),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”,在“生长”了2019次后形成的图形中所有正方形的面积和是( )

A.2018B.2019C.2020D.2021
【答案】C
【解析】
根据勾股定理和正方形的面积公式,知“生长”1次后,以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,即所有正方形的面积和是2×1=2;“生长”2次后,所有的正方形的面积和是3×1=3,推而广之即可求出“生长”2019次后形成图形中所有正方形的面积之和.
设直角三角形的是三条边分别是a,b,c.
根据勾股定理,得a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1,
所以,生长1次后,所有的正方形的面积和是2,
同理可得,生长2次后,所有的正方形的面积和是3,生长3次后,所有的正方形的面积和是4,所以,“生长”了2019次后形成的图形中所有的正方形的面积和是2020×1=2020.
故选C.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.

【题目】深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图中提供的信息,解答下列问题:
分组 | 频数 | 频率 |
74.5≤x<79.5 | 2 | 0.04 |
79.5≤x<84.5 | a | 0.16 |
84.5≤x<89.5 | 20 | 0.40 |
89.5≤x<94.5 | 16 | 0.32 |
94.5≤x<100.5 | 4 | b |
合计 | 50 | 1 |
(1)频数、频率分布表中a= ,b= ;
(2)补全频数分布直方图;
(3)初赛成绩在94.5≤x<100.5分的四位同学恰好是七年级、八年级各一位,九年级两位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,则所选两位同学恰好都是九年级学生的概率为 .