题目内容
【题目】已知,抛物线![]() 与x轴正半轴交于A、B两点(A点在B点左边),且AB=4.
与x轴正半轴交于A、B两点(A点在B点左边),且AB=4.
(1)求k值;
(2)该抛物线与直线![]() 交于C、D两点,求S△ACD;
交于C、D两点,求S△ACD;
(3)该抛物线上是否存在不同于A点的点P,使S△PCD=S△ACD?若存在,求出P点坐标.
(4)若该抛物线上有点P,使S△PCD=tS△ACD,抛物线上满足条件的P点有2个,3个,4个时,分别直接写出t的取值范围.
【答案】(1)k=4(2)![]() (3)存在符合条件的P点,且坐标为 P1(7,
(3)存在符合条件的P点,且坐标为 P1(7,![]() )、P2(
)、P2(![]() ,
,![]() )、P3(
)、P3(![]() ,
,![]() );(4)当0<t<
);(4)当0<t<![]() 时,P点有四个;当t=
时,P点有四个;当t=![]() 时,P点有三个;当t>
时,P点有三个;当t>![]() 时,P点有两个
时,P点有两个
【解析】
(1)设A(x1,0)、B(x2,0),x1、x2>0,根据题意可得AB=|x1﹣x2|=![]() =4,而x1+x2,x1x2可由k表达出来,根据等量关系即可求得k的值;
=4,而x1+x2,x1x2可由k表达出来,根据等量关系即可求得k的值;
(2)先联立直线CD和抛物线的解析式求出C,D两点的坐标,此时从图可看出△ACD是一个不规则的三角形,所以可过A作直线AE∥y轴,交直线CD于E,那么线段AE为底,C,D的横坐标差的绝对值为高即可得出△ACD的面积;
(3)设直线CD与y轴的交点为G,过点A作l1∥CD交y轴于H,取GH=GL,过L作l2∥CD交y轴于L,那么直线l1,l2到直线CD的距离等于点A到直线CD的距离,所以它们与抛物线的交点都是符合条件的P点;
(4)通过作图可以发现,在直线CD上方肯定有两个P点,所以只考虑直线CD下方的P点数,这就要抓住P点有三个或CD下方有一个P点的情况:P为平行于CD的直线与抛物线的唯一交点;若上述情况(P点有三个)中,t=![]() ,那么:P点有两个时,t>
,那么:P点有两个时,t>![]() ;P点有四个时,0<t<
;P点有四个时,0<t<![]() .
.
(1)设A(x1,0)、B(x2,0),且x1<x2,x1、x2>0,
则:x1+x2=2k,x1x2=2(k+2)=2k+4,
∴AB=|x1﹣x2|=![]() =4,即:k2﹣2k﹣8=0,
=4,即:k2﹣2k﹣8=0,
解得:k1=﹣2,k2=4,
∵x1+x2>0,即k>0,
∴k=4;
(2)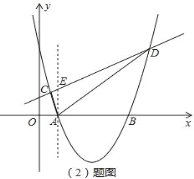
由(1)知,抛物线的解析式:y=![]() x2﹣4x+6,点A(2,0),B(6,0);
x2﹣4x+6,点A(2,0),B(6,0);
联立直线CD和抛物线的解析式,有:
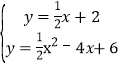 ,
,
解得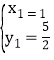 ,
,![]() ,
,
即:C(1,![]() ),D(8,6),
),D(8,6),
如图,过A作直线AE∥y轴,交直线CD于E,则E(2,3),AE=3,
S△ACD=![]() AE×|xD﹣xC|=
AE×|xD﹣xC|=![]() ×3×7=
×3×7=![]() ;
;
(3)如右图,设直线CD与y轴的交点为G,过点A作l1∥CD交y轴于H,取GH=GL,过L作l2∥CD交y轴于L;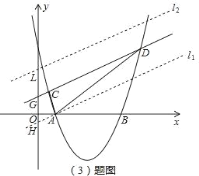
设直线l1:y=![]() x+b1,代入A(2,0),得:
x+b1,代入A(2,0),得:
![]() ×2+b1=0,b1=﹣1
×2+b1=0,b1=﹣1
即,直线l1:y=![]() x﹣1,H(0,﹣1),GL=GH=3,L(0,5);
x﹣1,H(0,﹣1),GL=GH=3,L(0,5);
同上,可求得,直线l2:y=![]() x+5;
x+5;
联立直线l1与抛物线的解析式,得:
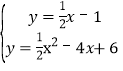 ,
,
解得![]() ,
,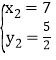 ,
,
即:P1(7,![]() );
);
联立直线l2与抛物线的解析式,得:
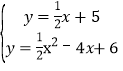 ,
,
解得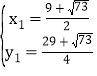 ,
,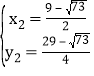 ,
,
即:P2(![]() ,
,![]() )、P3(
)、P3(![]() ,
,![]() );
);
综上,存在符合条件的P点,且坐标为 P1(7,![]() )、P2(
)、P2(![]() ,
,![]() )、P3(
)、P3(![]() ,
,![]() );
);
(4)当满足条件的P点有三个时,如右图: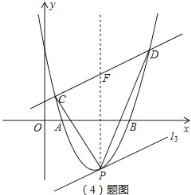
直线l3∥CD,且直线l3与抛物线只有唯一交点P;
设直线l3:y=![]() x+b3,联立抛物线的解析式有:
x+b3,联立抛物线的解析式有:
![]() x+b3=
x+b3=![]() x2﹣4x+6,即:x2﹣9x+12﹣2b3=0
x2﹣4x+6,即:x2﹣9x+12﹣2b3=0
△=81﹣4×(12﹣2b3)=0,解得:b3=﹣![]()
即,直线l3:y=![]() x﹣
x﹣![]() ,P(
,P(![]() ,﹣
,﹣![]() );
);
过点P作直线PF∥y轴,交直线CD于F,则F(![]() ,
,![]() )、PF=
)、PF=![]() ,
,
S△PCD=![]() PF×|yD﹣yC|=
PF×|yD﹣yC|=![]() ×
×![]() ×7=
×7=![]() ,t=
,t=![]() =
=![]() =
=![]() ,
,
综上上面的计算结果和图形来看:
当0<t<![]() 时,P点有四个;
时,P点有四个;
当t=![]() 时,P点有三个;
时,P点有三个;
当t>![]() 时,P点有两个.
时,P点有两个.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案






