题目内容
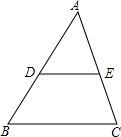已知：如图，DE∥BC，且
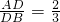，那么△ADE与△ABC的面积比S△ADE：S△ABC=
- A.2：5
- B.2：3
- C.4：9
- D.4：25
D
分析：由于DE∥BC，易证得△ADE∽△ABC，已知AD、BD的比例关系，即可得到AD、AB的比例关系即两个三角形的相似比；根据相似三角形的面积比等于相似比的平方，即可判断出正确的结论．
解答：∵AD：BD=2：3，
∴AD：AB=2：5；
∵DE∥BC，
∴△ADE∽△ABC；
∴
=（
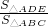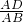）2=
；
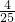故选D．
点评：此题主要考查的是相似三角形的性质：相似三角形的面积比等于相似比的平方．
分析：由于DE∥BC，易证得△ADE∽△ABC，已知AD、BD的比例关系，即可得到AD、AB的比例关系即两个三角形的相似比；根据相似三角形的面积比等于相似比的平方，即可判断出正确的结论．
解答：∵AD：BD=2：3，
∴AD：AB=2：5；
∵DE∥BC，
∴△ADE∽△ABC；
∴
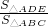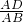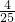=（）2=；故选D．
点评：此题主要考查的是相似三角形的性质：相似三角形的面积比等于相似比的平方．
练习册系列答案
53随堂测系列答案
相关题目
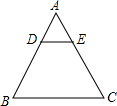已知：如图，DE是△ABC的中位线，若AD=4，AE=5，BC=12，则△ADE的周长为（ ）| A、7.5 | B、15 | C、30 | D、24 |
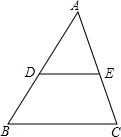已知：如图，DE∥BC，且| AD |
| DB |
| 2 |
| 3 |
| A、2：5 | B、2：3 |
| C、4：9 | D、4：25 |
16、请把下列证明过程补充完整：
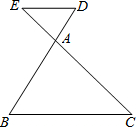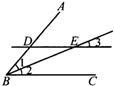
已知：如图，DE∥BC交BA的延长线于D，交CA的延长线于E，AD=4，DB=12，DE=3．求BC的长．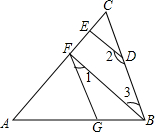
已知：如图，DE⊥AC，∠AGF=∠ABC，∠1=20°，∠2=160°，试判断BF与AC的位置关系，并说明理由．