题目内容
 已知:如图,DE⊥AC,∠AGF=∠ABC,∠1=20°,∠2=160°,试判断BF与AC的位置关系,并说明理由.
已知:如图,DE⊥AC,∠AGF=∠ABC,∠1=20°,∠2=160°,试判断BF与AC的位置关系,并说明理由.分析:首先证明FG∥BC可得∠1=∠3,再证明BF∥DE进而得到∠DEA=∠BFA,然后再证明∠AED=90°即可.
解答:解:BF⊥AC,
理由如下:∵∠AGF=∠ABC,
∴FG∥BC,
∴∠1=∠3.
∵∠1=20°,
∴∠3=20°,
∵∠2=160°,
∴∠2+∠3=180°,
∴BF∥DE.
∴∠DEA=∠BFA,
∵DE⊥AC,
∴∠AFB=90°,
∴∠AED=90°,
∴BF⊥AC.
理由如下:∵∠AGF=∠ABC,
∴FG∥BC,
∴∠1=∠3.
∵∠1=20°,

∴∠3=20°,
∵∠2=160°,
∴∠2+∠3=180°,
∴BF∥DE.
∴∠DEA=∠BFA,
∵DE⊥AC,
∴∠AFB=90°,
∴∠AED=90°,
∴BF⊥AC.
点评:此题主要考查了平行线的判定与性质,关键是掌握两直线平行,同位角相等,内错角相等.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
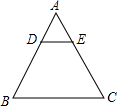 已知:如图,DE是△ABC的中位线,若AD=4,AE=5,BC=12,则△ADE的周长为( )
已知:如图,DE是△ABC的中位线,若AD=4,AE=5,BC=12,则△ADE的周长为( )| A、7.5 | B、15 | C、30 | D、24 |
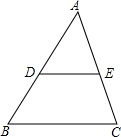 已知:如图,DE∥BC,且
已知:如图,DE∥BC,且| AD |
| DB |
| 2 |
| 3 |
| A、2:5 | B、2:3 |
| C、4:9 | D、4:25 |
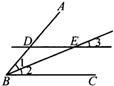 16、请把下列证明过程补充完整:
16、请把下列证明过程补充完整: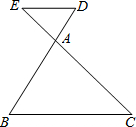 已知:如图,DE∥BC交BA的延长线于D,交CA的延长线于E,AD=4,DB=12,DE=3.求BC的长.
已知:如图,DE∥BC交BA的延长线于D,交CA的延长线于E,AD=4,DB=12,DE=3.求BC的长.