题目内容
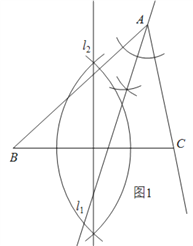
【题目】如图,△ABC.
(1)用直尺和圆规作∠A的平分线所在的直线![]() 和边BC的垂直平分线
和边BC的垂直平分线![]() (要求:不写作法,保留画图痕迹);
(要求:不写作法,保留画图痕迹);
(2)设(1)中的直线![]() 和直线
和直线![]() 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.

【答案】(1)作图见解析;(2)证明见解析.
【解析】试题分析:
(1)如图1,用“尺规作图”作出∠ABC的角平分线,再反向延长即可得到![]() ;再用“尺规作图”作出BC的垂直平分线
;再用“尺规作图”作出BC的垂直平分线![]() 即可;
即可;
(2)如图2,连接PB、PC,由题意易证△PBE≌△PCF,从而可得BE=CF.
试题解析:
(1)如图1,图中直线![]() 和直线
和直线![]() 为题中所求直线;
为题中所求直线;
(2)如图2,连接PB、PC,
∵AP平分∠BAC,PE⊥AB于点E,PF⊥AC于点F,
∴PE=PF,∠PEB=∠PFC=90°,
∵![]() 垂直平分BC,点P在
垂直平分BC,点P在![]() 上,
上,
∴PB=PC,
∴△PBE≌△PCF,
∴BE=CF.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案【题目】为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时) | 0 | 1 | 2 | 3 | … |
油箱剩余油量 Q(升) | 100 | 94 | 88 | 82 | … |
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).
【题目】某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
A | B | |
载客量(人/辆) | 40 | 20 |
租金(元/辆) | 200 | 150 |
(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?



