Question

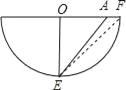
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA＝2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm．

Answer 1

【答案】2

【解析】试题分析：因为OE=OF=EF=10（cm），

所以底面周长=10π（cm），

将圆锥侧面沿OF剪开展平得一扇形，此扇形的半径OE=10（cm），弧长等于圆锥底面圆的周长10π（cm）

设扇形圆心角度数为n，则根据弧长公式得：

10π=，

所以n=180°，

即展开图是一个半圆，

因为E点是展开图弧的中点，

所以∠EOF=90°，

连接EA，则EA就是蚂蚁爬行的最短距离，

在Rt△AOE中由勾股定理得，

EA2=OE2+OA2=100+64=164，

所以EA=2（cm），

即蚂蚁爬行的最短距离是2（cm）．