题目内容
【题目】如图，在平面直角坐标系中，点P(1，5)、Q(m，n)在反比例函数的图象上，过点P分别作x轴、y轴的垂线，垂足分别为A、B，点Q为图象上的动点，过点Q分别作x轴、y轴的垂线，垂足分别为C、D，两垂线相交于点E，随着m的增大，四边形OCQD与四边形OAPB不重合的面积变化为( )
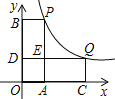
A. 先增大后减小 B. 先减小后增大 C. 先减小后增大再减小 D. 先增大后减小再增大
【答案】B
【解析】
根据重合部分是矩形，分成Q在P的左侧和右侧两种情况进行讨论，依据矩形的面积公式即可判断．
解：矩形OAPB，矩形OCQD的面积不变．当点Q在点P的左边时，随着m的增大，两矩形重合部分的小矩形的长不变，宽变大，所以重合面积变大，所以不重合的面积变小；当Q在P的右侧时，重合部分宽不变，而长减小，因而重合面积减小，所以不重合的面积变大．所以随着m的增大，四边形OCQD与四边形OAPB不重合的面积变化为先减小后增大；
故选：B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
