Question

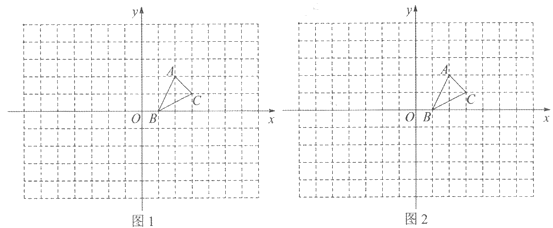
【题目】已知，在等腰△ABC中，AB＝AC，AD⊥BC于点D，以AC为边作等边△ACE，直线BE交直线AD于点F．如图，60°≤∠BAC≤120°，△ACF与△ABC在直线AC的同侧．

（1）①补全图形；

②∠EAF+∠CEF＝　 　；

（2）猜想线段FA，FB，FE的数量关系，并证明你的结论；

（3）若BC＝2，则AF的最大值为　 　．

Answer 1

【答案】（1）①图形如图 1 所示；②结论：∠EAF+∠CEF=60°，理由见解析；（2）结论：FA=FE+FB．理由见解析；（3）AF 的最大值为．

【解析】

（1）①根据要求画出图形，如图1所示；
②结论：∠EAF+∠CEF=60°如图1中，以A为圆心，AB为半径画圆．作AH⊥BE于H．首先证明∠EBC=∠FAH=30°，根据三角形的内角和定理和外角的性质即可解决问题；
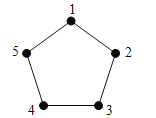
（2）结论：FA=FE+FB．如图2中，在FA上取一点K，使得FK=FE，连接EK．只要证明△AEK≌△CEF（SAS），即可解决问题；
（3）因为60°≤∠BAC≤120°，所以观察图象可知，当∠BAC=60°时，AF的值最大，求出AD，DF即可解决问题；

（1）①图形如图 1 所示；

②结论：∠EAF+∠CEF=60°

理由：如图 1 中，以 A 为圆心，AB 为半径画圆．作 AH⊥BE 于 H．

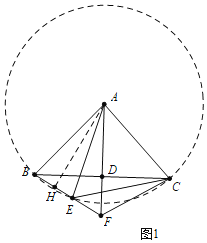
∵AB=AC=AE，

∴B，E，C 在⊙A 上，

∵△AEC 是等边三角形，

∴∠EAC=60°，

∴∠EBC=EAC=30°，

∵AB=AE，AH⊥BE，

∴∠EAH= ∠BAE，

∵∠BCE= ∠BAE，

∴∠BCE=∠EAH，

∴AD⊥BC，

∴∠BDF=∠AHF=90°，∠BFD=60°，

∴∠HAF=30°，

∴∠EAF+∠CEF=∠EAF+∠EBC+∠BCE=∠EAF+∠EAH+∠EBC=30°+30°=60°．

（2）结论：FA=FE+FB．

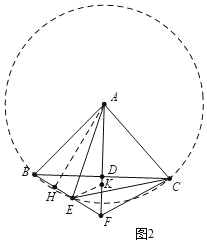
理由：如图 2 中，在 FA 上取一点 K，使得 FK=FE，连接 EK．

∵FE=CK，∠EFK=60°，

∴△EFK 是等边三角形，

∴EK=EF，∠EKF=∠KEF=60°，

∵∠AEC=∠KEF=60°，

∴∠AEK=∠CEF，

∵AE=EC，EK=EF，

∴△AEK≌△CEF（SAS），

∴AK=FC，

∵AD 垂直平分线段 BC，

∴FB=CF，

∴FA=FK+AK=FE+FC=FE+FB．

如图 3 中．

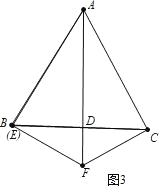
∵60°≤∠BAC≤120°，

观察图象可知，当∠BAC=60°时，AF 的值最大， 此时∵AB=AC=BC=2，AF⊥BC，

∴AD=ABsin60°=，DF=BDtan30°= ，

∴AF=+= ，

∴AF 的最大值为．