题目内容
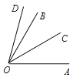
【题目】如图，∠COD=45°，∠BOD=
∠COD，OC是∠AOB的平分线，求∠AOD的度数．
【答案】75°.
【解析】
解法一：先根据∠COD=45°，∠BOD=
∠COD求出∠BOD，∠COB的度数，再利用角平分线可求出∠AOB，最后利用∠AOD=∠BOD＋∠AOB即可求解.
解法二：先根据∠COD=45°，∠BOD=∠COD求出∠BOD，∠COB的度数，再利用角平分线可求出∠AOC的度数，最后利用∠AOD=∠COD＋∠AOC即可求解.
解法一：∵∠COD=45°，∠BOD=∠COD,
∴∠BOD=×45° =15°．
∴∠COB=∠COD-∠BOD=45°-15°=30°．
∵OC是∠AOB的平分线，
∴∠AOB=2∠COB=2×30°=60°
∴∠AOD=∠BOD＋∠AOB=15°＋60°=75°．
解法二：∵∠COD=45°，∠BOD=∠COD,
∴∠BOD=×45° =15°．
∴∠COB=∠COD-∠BOD=45°-15°=30°．
∵OC是∠AOB的平分线，
∴∠AOC=∠COB=30°
∴∠AOD=∠COD＋∠AOC=45°＋30°=75°
练习册系列答案
相关题目
