题目内容
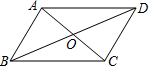
如图，Rt△ABC中，∠ACB=90°，AC=
，BC=1，将Rt△ABC绕C点旋转90°后为Rt△A′B′C′，再将Rt△A′B′C′绕B点旋转为Rt△A″B″C″使得A、C、B′、A″在同一直线上，则A点运动到A″点所走的长度为______．
| 3 |
第一次是以点C为圆心，AC为半径，旋转的度数是90度，
第二次是以点B′为圆心，AB为半径，旋转的度数是180°-60°=120°；
所以根据弧长公式可得：
=(
+
)π．
第二次是以点B′为圆心，AB为半径，旋转的度数是180°-60°=120°；
所以根据弧长公式可得：
90π×
| ||
| 180 |
| ||
| 2 |
| 4 |
| 3 |
练习册系列答案
备战中考寒假系列答案
相关题目
