ЬтФПФкШн
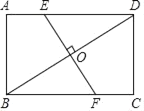
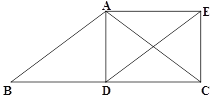
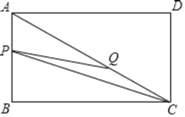
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН3ЃЌBCЃН4ЃЎЕуPДгЕуAГіЗЂЃЌбиAЉBЉCдЫЖЏЃЌЫйЖШЮЊУПУы1ИіЕЅЮЛГЄЖШЃЎЕуQДгЕуCГіЗЂЃЌбиCЉAЉDдЫЖЏЃЌбиCЉAдЫЖЏЪБЕФЫйЖШЮЊУПУы1ИіЕЅЮЛГЄЖШЃЌбиAЉDдЫЖЏЪБЕФЫйЖШЮЊУПУы3ИіЕЅЮЛГЄЖШЃЎPЁЂQСНЕуЭЌЪБГіЗЂЃЌЕБЕуQЕНДяЕуDЪБЃЌPЁЂQСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎСЌНсPQЁЂCPЃЎЩшЁїAPQЕФУцЛ§ЮЊSЃЌЕуPЕФдЫЖЏЪБМфЮЊtЃЈУыЃЉЃЎ
ЃЈ1ЃЉЕБtЃН6ЪБЃЌЧѓAQЕФГЄЃЎ
ЃЈ2ЃЉЕБЕуQбиCЉAдЫЖЏЪБЃЌгУКЌtЕФДњЪ§ЪНБэЪОЕуQЕНABЁЂBCЕФОрРыЃЎ
ЃЈ3ЃЉЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ4ЃЉдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌжБНгаДГіЁїAPQгыЁїCPQЭЌЪБЮЊЖлНЧШ§НЧаЮЪБtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉAQЃН3;ЃЈ2ЃЉЕуQЕНABЕФОрРыЃК![]() ;ЕуQЕНBCЕФОрРыЃК
;ЕуQЕНBCЕФОрРыЃК![]() ;ЃЈ3ЃЉМћНтЮі;ЃЈ4ЃЉМћНтЮі.
;ЃЈ3ЃЉМћНтЮі;ЃЈ4ЃЉМћНтЮі.
ЁОНтЮіЁП
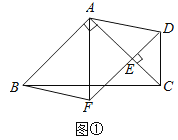
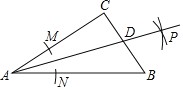
ЃЈ1ЃЉШчЭМ1жаЃЌЛГіЭМаЮЧѓГіAQМДПЩЃЛ
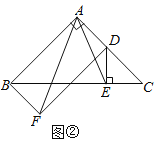
ЃЈ2ЃЉШчЭМ2жаЃЌQMЁЭABгкMЃЌQNЁЭBCгкNЃЎдђЫФБпаЮMBNQЪЧОиаЮЃЌПЩЕУQM=BNЃЌQNЁЮABЃЌЭЦГі![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
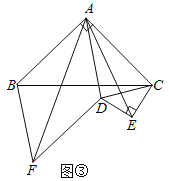
ЃЈ3ЃЉЗжШ§жжЧщаЮЧѓНтЂйШчЭМ3жаЃЌЕБ0ЃМtЁм3ЪБЃЌЂкШчЭМ4жаЃЌЕБ3ЃМtЁм5ЪБЃЌЂлШчЭМ5жаЃЌЕБ5ЃМtЁм![]() ЪБЃЛ
ЪБЃЛ
ЃЈ4ЃЉЧѓГіШ§ИіЬиЪтЮЛжУЕФtЕФжЕМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉШчЭМ1жаЃЌ
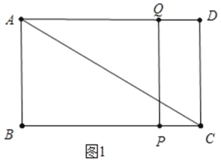
дкRtЁїACBжаЃЌACЃН![]() ЃН
ЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁрtЃН6ЪБЃЌЕуQдкADЪБЃЌ
AQЃН3ЃЈtЉ5ЃЉЃН3ЁСЃЈ6Љ5ЃЉЃН3ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌQMЁЭABгкMЃЌQNЁЭBCгкNЃЎдђЫФБпаЮMBNQЪЧОиаЮЃЌ
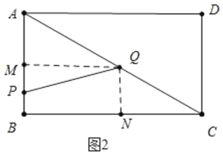
ЁрQMЃНBNЃЌQNЁЮABЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрQNЃН![]() tЃЌCNЃН
tЃЌCNЃН![]() tЃЌ
tЃЌ
ЁрQMЃНBMЃН4Љ![]() tЃЎ
tЃЎ
ЁрЕуQЕНABЕФОрРыЃК4-![]() tЃЎ
tЃЎ
ЕуQЕНBCЕФОрРыЃК![]() tЃЛ
tЃЛ
ЃЈ3ЃЉЂйШчЭМ3жаЃЌЕБ0ЃМtЁм3ЪБЃЌ
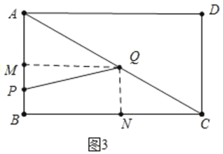
SЃН![]() APQMЃН
APQMЃН![]() tЃЈ4Љ
tЃЈ4Љ![]() tЃЉЃНЉ
tЃЉЃНЉ![]() t2+2tЃЎ
t2+2tЃЎ
ЂкШчЭМ4жаЃЌЕБ3ЃМtЁм5ЪБЃЌ
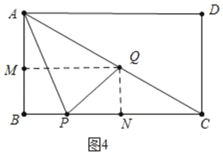
SЃНSЁїABCЉSЁїABPЉSЁїQPCЃН![]() ЁС3ЁС4Љ
ЁС3ЁС4Љ![]() ЁСЃЈ7ЉtЃЉ
ЁСЃЈ7ЉtЃЉ![]() tЉ
tЉ![]() ЃЈtЉ3ЃЉЁС3ЃН
ЃЈtЉ3ЃЉЁС3ЃН![]() t2Љ
t2Љ![]() t+
t+![]() ЃЎ
ЃЎ
ЂлШчЭМ5жаЃЌЕБ5ЃМtЁм![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
ЃЈ4ЃЉШчЭМ6жаЃЌ
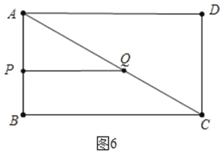
ЕБPQЁЮBCЪБЃЌ
ЁпAPЃКABЃНAQЃКACЃЌ
ЁрtЃК3ЃНЃЈ5ЉtЃЉЃК5ЃЌНтЕУtЃН![]() ЃЌ
ЃЌ
ШчЭМ7жаЃЌ
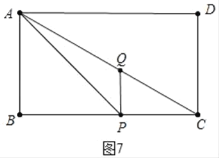
ЕБPQЁЮABЪБЃЌCPЃКCBЃНCQЃКCAЃЌ
ЁрЃЈ7ЉtЃЉЃК4ЃНtЃК5ЃЌНтЕУtЃН![]() ЃЌ
ЃЌ
ШчЭМ8жаЃЌ
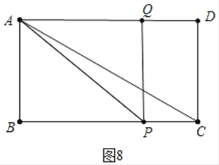
ЕБAQЃНBPЪБЃЌ3ЃЈtЉ5ЃЉЃНtЉ3ЃЌНтЕУtЃН6ЃЌ
ЁрЕБ0ЃМtЃМ![]() Лђ
Лђ![]() ЃМtЃМ5Лђ5ЃМtЃМ6ЪБЃЌЁїAPQгыЁїCPQЭЌЪБЮЊЖлНЧШ§НЧаЮЃЎ
ЃМtЃМ5Лђ5ЃМtЃМ6ЪБЃЌЁїAPQгыЁїCPQЭЌЪБЮЊЖлНЧШ§НЧаЮЃЎ

 ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИ
ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИ ГЄНзївЕБОЭЌВНСЗЯАВсЯЕСаД№АИ
ГЄНзївЕБОЭЌВНСЗЯАВсЯЕСаД№АИЁОЬтФПЁПЁАТЬЫЎЧрЩНОЭЪЧН№ЩНвјЩНЁБЃЌЮЊБЃЛЄЩњЬЌЛЗОГЃЌAЃЌBСНДхзМБИИїздЧхРэЫљЪєЧјгђбјгуЭјЯфКЭВЖгуЭјЯфЃЌУПДхВЮМгЧхРэШЫЪ§МАзмПЊжЇШчЯТБэЃК
ДхзЏ | ЧхРэбјгуЭјЯфШЫЪ§/ШЫ | ЧхРэВЖгуЭјЯфШЫЪ§/ШЫ | змжЇГі/дЊ |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
ЃЈ1ЃЉШєСНДхЧхРэЭЌРргцОпЕФШЫОљжЇГіЗбгУвЛбљЃЌЧѓЧхРэбјгуЭјЯфКЭВЖгуЭјЯфЕФШЫОљжЇГіЗбгУИїЪЧЖрЩйдЊЃЛ
ЃЈ2ЃЉдкШЫОљжЇГіЗбгУВЛБфЕФЧщПіЯТЃЌЮЊНкдМПЊжЇЃЌСНДхзМБИГщЕї40ШЫЙВЭЌЧхРэбјгуЭјЯфКЭВЖгуЭјЯфЃЌвЊЪЙзмжЇГіВЛГЌЙ§102000дЊЃЌЧвЧхРэбјгуЭјЯфШЫЪ§аЁгкЧхРэВЖгуЭјЯфШЫЪ§ЃЌдђгаФФМИжжЗжХфЧхРэШЫдБЗНАИЃП