题目内容
【题目】如图，在一块正方形ABCD木板上要贴三种不同的墙纸，正方形EFCG部分贴A型墙纸，△ABE部分贴B型墙纸，其余部分贴C型墙纸．A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元．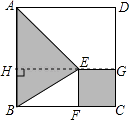
（1）探究1：如果木板边长为1米，FC= 
米，则一块木板用墙纸的费用需元；
（2）探究2：如果木板边长为2米，正方形EFCG的边长为x米，一块木板需用墙纸的费用为y元，
①用含x的代数式表示y（写过程）．
②如果一块木板需用墙纸的费用为225元，求正方形EFCG的边长为多少米？
【答案】
（1）55
（2）解：①∵木板边长为2米，
∴木板的面积为：4平方米．
∵正方形EFCG的边长为x米，
∴S正方形EFCG=x2 ， S△ABE=2﹣x，
∴空白的面积为：4﹣x2﹣（2﹣x）=2﹣x2+x，
y=60x2+80（2﹣x）+40（2﹣x2+x），
y=20x2﹣40x+240
②当y=225时，
225=20x2﹣40x+240，解得：
x1= 
，x2= 
∴正方形EFCG的边长为 或 米
【解析】（1）解：探究1：∵四边形ABCD是正方形，
∴AB=BC=CD=DA=1，
∴S正方形ABCD=1，
∵四边形EFCG是正方形，
∴EF=CF= ，
∴S正方形EFCG= 
，BF= ，
∴S△ABE=
∴空白部分的面积为：1﹣ ﹣ = ，
∴这块木板用墙纸的费用为： .60+ .80+40× =55元．
所以答案是：55．
【考点精析】本题主要考查了三角形的面积和正方形的性质的相关知识点，需要掌握三角形的面积=1/2×底×高；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．
