Question

【题目】已知AB//CD，点E为平面内一点，BE⊥CE于E

（1）如图1，请直接写出∠ABE和∠DCE之间的数量关系

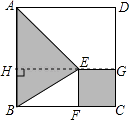
（2）如图2，过点E作EF⊥CD，垂足为F，求证：∠CEF=∠ABE

（3）如图3，在（2）的条件下，作EG平分∠CEF，交DF于点G，作ED平分∠BEF，交CD于D，连接BD，若∠DBE＋∠ABD＝180°，且∠BDE＝3∠GEF，求∠BEG的度数．

Answer 1

【答案】（1）∠ECD＝90°＋∠ABE；（2）见解析；（3）105°

【解析】

（1）如图1中，从BE交DC的延长线于H．利用三角形内角和定理即可证明；

（2）只要证明∠CEF与∠CEM互余，∠BEM与∠CEM互余，可得∠CEF＝∠BEM即可解决问题；

（3）如图3中，设∠GEF＝，∠EDF＝．想办法构建方程求出即可解决问题；

（1）结论：∠ECD＝90°＋∠ABE．

理由：如图1中，延长BE交DC的延长线于H．

∵AB∥CH，

∴∠ABE＝∠H，

∵BE⊥CE，

∴∠CEH＝90°，

∴∠ECH＝180°∠CEH∠H＝180°90°∠H＝90°∠H，

∴∠ECD＝180°∠ECH＝180°（90°∠H）＝90°＋∠H，

∴∠ECD＝90°＋∠ABE．

（2）如图2中，作EM∥CD，

∵EM∥CD，CD∥AB，

∴AB∥CD∥EM，

∴∠BEM＝∠ABE，∠F＋∠FEM＝180°，

∵EF⊥CD，

∴∠F＝90°，

∴∠FEM＝90°，

∴∠CEF与∠CEM互余，

∵BE⊥CE，

∴∠BEC＝90°，

∴∠BEM与∠CEM互余，

∴∠CEF＝∠BEM，

∴∠CEF＝∠ABE．

（3）如图3中，设∠GEF＝，∠EDF＝．

∴∠BDE＝3∠GEF＝3，

∵EG平分∠CEF，

∴∠CEF＝2∠FEG＝2，

∴∠ABE＝∠CEF＝2，

∵AB∥CD∥EM，

∴∠MED＝∠EDF＝，∠KBD＝∠BDF＝3＋，∠ABD＋∠BDF＝180°，

∴∠BED＝∠BEM＋∠MED＝2＋，

∵ED平分∠BEF，

∴∠BED＝∠FED＝2＋，

∴∠DEC＝，

∵∠BEC＝90°，

∴2＋2＝90°，

∵∠DBE＋∠ABD＝180°，∠ABD＋∠BDF＝180°，

∴∠DBE＝∠BDF＝∠BDE＋∠EDF＝3＋，

∵∠ABK＝180°，

∴∠ABE＋∠B＝DBE＋∠KBD＝180°，

即2＋（3＋）＋（3α＋）＝180°，

∴6＋（2＋2）＝180°，

∴＝15°，

∴∠BEG＝∠BEC＋∠CEG＝90°＋15°＝105°．