题目内容
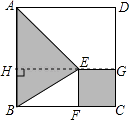
【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
【答案】C
【解析】
在Rt△ABC中利用勾股定理可求出AC=10,设BE=a,则CE=8﹣a,根据折叠的性质可得出BE=FE=a,AF=AB=6,∠AFE=∠B=90°,进而可得出FC=4,在Rt△CEF中,利用勾股定理可得出关于a的一元二次方程,解之即可得出a值,将其代入8﹣a中即可得出线段CE的长度.
解:在Rt△ABC中,AB=6,BC=8,
∴AC=10.
设BE=a,则CE=8﹣a,
根据翻折的性质可知,BE=FE=a,AF=AB=6,∠AFE=∠B=90°,
∴FC=4.
在Rt△CEF中,EF=a,CE=8﹣a,CF=4,
∴CE2=EF2+CF2,即(8﹣a)2=a2+42,
解得:a=3,
∴8﹣a=5.
故选:C.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目