题目内容
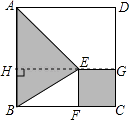
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)设点![]() 是
是![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
①若![]() ,求点
,求点![]() 的坐标;
的坐标;
②若![]() 的面积为
的面积为![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() 或
或![]()
【解析】
(1)先确定出点B坐标和点A坐标,进而求出点C坐标,最后用待定系数法求出直线BC解析式;
(2) ①设点M(x,0),则点P(x,![]() x+3),
x+3),![]() 、
、![]() 均为直角三角形结合勾股定理,求解
均为直角三角形结合勾股定理,求解![]() 点横坐标;
点横坐标;
②先表示出PQ,最后用三角形面积公式即可得出结论.
解:(1)对于![]() ,
,
由x=0得:y=3,
∴B(0,3)
由y=0得:![]() x+3=0,解得x=6,
x+3=0,解得x=6,
∴A(6,0),
∵点C与点A关于y轴对称
∴C(6,0)
设直线BC的函数解析式为y=kx+b
则![]() ,
,
解得 ,
,
∴直线BC的函数解析式为y= ![]() x+3.
x+3.
(2) ①设点M(x,0),则点P(x,![]() x+3),
x+3),
∵∠MBC=90,
∴△BMC是直角三角形,
∴BM2+BC2=MC2
∵BM2=OM2+OB2=x2+92,BC2=OC2+OB2=62+32=45,MC2=(6-x)2,
∴x2+9+45=(6-x)2,
解得x=-![]() ,
,
∴p![]() ;
;
②如图1,

设M(x,0),
∵点P在直线AB上,
∴P(x, ![]() x+3),
x+3),
∵点Q在直线CB上:y=![]() x+3上
x+3上
∴Q(x,![]() x+3)
x+3)
过点B作BD⊥PQ于点D,
∴PQ=|![]() x+3(
x+3(![]() x+3)|=|x|,
x+3)|=|x|,
∵BD=OM=|x|
∴S△PQB=![]() PQBD=
PQBD=![]() x2=
x2=![]() ,
,
解得x=±![]() ,
,
∴M(![]() ,0)或M(
,0)或M(![]() ,0).
,0).

练习册系列答案
相关题目