题目内容
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.
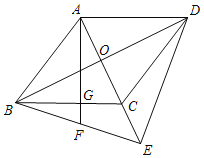
(1)求证:EB=ED;
(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,
①试判断△ABF的形状,并加以证明;
②设CE=m,求EF的长(用含m的式子表示).
【答案】(1)见解析;(2)①△ABF是等腰三角形(AB=AF),理由见解析;②EF=![]() m
m
【解析】
(1)只要证明AE垂直平分线段BD即可;
(2)①利用等腰直角三角形的判定和性质,以及同角的余角相等,想办法证明∠ABF=∠AFB即可;
②作EH⊥AF交AF的延长线于H.根据解直角三角形,想办法求出FH、EH的长度,即可解决问题;
(1)证明:∵四边形ABCD是菱形,
∴EA⊥BD,OB=OD,
∴EB=ED
(2)解:①结论:△ABF是等腰三角形(AB=AF);
理由:∵∠AEB=45°,EO⊥OB,
∴△BOE是等腰直角三角形,
∴∠OBE=∠OEB=45°,
∵AG⊥BC,
∴∠AGB=∠BOC=90°,
∴∠GAC+∠ACB=90°,∠ACB+∠OBC=90°,
∴∠CAG=∠CBO=∠ABO,
∵∠ABF=∠ABO+∠OBE=∠ABO+45°,∠AFB=∠CAG+∠AEB=∠CAG+45°,
∴∠AFB=∠ABF,
∴AB=AF,
∴△ABF是等腰三角形.
②作EH⊥AF交AF的延长线于H.
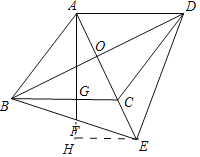
由题意CE=OC=OA=m,OB=AC═OD=2m,AE=3m,AB=AF=![]() m,
m,
tan∠CBO=tan∠CAG=![]() =
=![]() ,
,
∴EH=![]() m,AH=
m,AH=![]() m,
m,
∴FH=AH﹣AF=![]() m,
m,
在Rt△EFH中,EF=![]()
![]() m.
m.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | ▲ | ▲ | 25 |
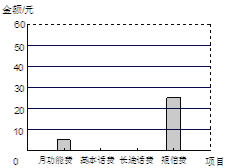
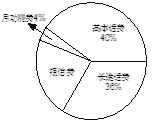
(1)该月小王手机话费共有多少元?
(2)扇形统计图中,表示短信费的扇形的圆心角为多少度?
(3)请将表格补充完整;
(4)请将条形统计图补充完整.