题目内容
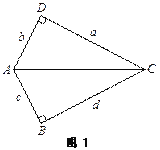
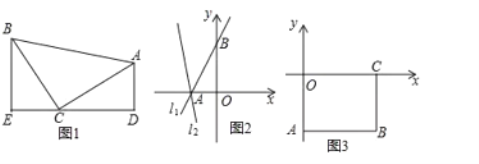
【题目】某数学兴趣小组，利用树影测量树高，如图（1），已测出树AB的影长AC为12米，并测出此时太阳光线与地面成30°夹角．
（1）求出树高AB；
（2）因水土流失，此时树AB沿太阳光线方向倒下，在倾倒过程中，树影长度发生了变化，假设太阳光线与地面夹角保持不变．求树的最大影长．（用图（2）解答）
【答案】（1）树AB的高约为4
m；（2）8m.
【解析】
（1）AB=ACtan30°=12×
=
（米）．
答：树高约为米．
（2）如图（2），B1N=AN=AB1sin45°=×
=
（米）．
NC1=NB1tan60°=×=
（米）．
AC1=AN+NC1=+．
当树与地面成60°角时影长最大AC2（或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大）
AC2=2AB2=
；
（1）在直角△ABC中，已知∠ACB=30°，AC=12米．利用三角函数即可求得AB的长；
（2）在△AB1C1中，已知AB1的长，即AB的长，∠B1AC1=45°，∠B1C1A=30°．过B1作AC1的垂线，在直角△AB1N中根据三角函数求得AN，BN；再在直角△B1NC1中，根据三角函数求得NC1的长，再根据当树与地面成60°角时影长最大，根据三角函数即可求解．
【题目】某市地铁二号线某工段需要开挖土石方，计划每小时挖掘土石方700m3，现决定向一大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如下表：
租金(单位：元/台·时) | 土石方量(单位：m3/台·时) | |
甲型挖掘机 | 90 | 50 |
乙型挖掘机 | 100 | 60 |
⑴ 若租用甲、乙两种型号的挖掘机共13台，恰好完成每小时的挖掘量，则甲、乙两种型号的挖掘机各需多少台？
⑵ 如果每小时支付的租金不超过1200元，又恰好完成每小时的挖掘量，那么共有哪几种不同的租用方案?
