题目内容
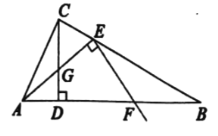
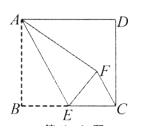
【题目】如图,正方形纸片![]() 的边长为5,E是边
的边长为5,E是边![]() 的中点,连接
的中点,连接![]() .沿
.沿![]() 折叠该纸片,使点B落在F点.则
折叠该纸片,使点B落在F点.则![]() 的长为______________________.
的长为______________________.
【答案】![]()
【解析】
根据折叠的性质结合三角形外角的性质可证得AE∥FC,利用勾股定理求得![]() 的长,根据Rt△EBG∽Rt△EAB,即可求得
的长,根据Rt△EBG∽Rt△EAB,即可求得![]() 的长,根据三角形中位线的性质即可求解.
的长,根据三角形中位线的性质即可求解.
根据折叠的性质,△ABE![]() △BFE,AE垂直平分BF,且E是边BC的中点,
△BFE,AE垂直平分BF,且E是边BC的中点,
∴BE=EF=EC,∠BEA=∠FEA,
∴∠EFC=∠ECF,
∵∠BEF =∠BEA+∠FEA=∠EFC+∠ECF,
∴∠BEA=∠ECF,
∴AE∥FC,
∵四边形![]() 是边长为5的正方形,且E是边BC的中点,
是边长为5的正方形,且E是边BC的中点,
∴∠ABC=90![]() ,AB=5,BE=
,AB=5,BE=![]() ,
,
∴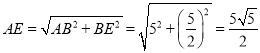 ,
,
连接BF交AE于点G,如图:
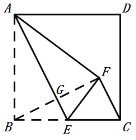
∵AE垂直平分BF,
∴∠BGE=90![]() ,
,
∴Rt△EBG∽Rt△EAB,
∴![]() ,即
,即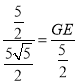 ,
,
∴![]() ,
,
∵GE∥FC,E是边BC的中点,
∴CF=2GE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目