题目内容
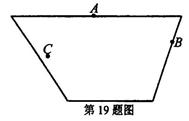
已知,如图,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系,A、B、C三点的坐标分别为A(8,0),B(8,10),C(0,4),
点D为线段BC的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为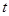 秒.
秒.
(1)求直线BC的解析式;
(2)若动点P在线段OA上移动,当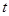 为何值时,四边形OPDC的面积是梯形COAB面积的
为何值时,四边形OPDC的面积是梯形COAB面积的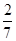 ?
?
(3)动点P从点O出发,沿折线OABD的路线移动过程中,设△OPD的面积为S,请直接写出S与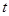 的函数关系式,并写出自变量
的函数关系式,并写出自变量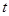 的取值范围。
的取值范围。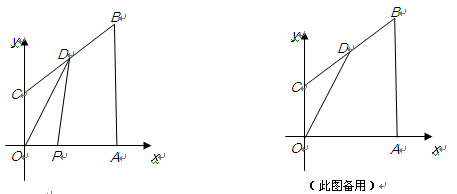
点D为线段BC的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为
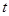 秒.
秒.(1)求直线BC的解析式;
(2)若动点P在线段OA上移动,当
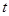 为何值时,四边形OPDC的面积是梯形COAB面积的
为何值时,四边形OPDC的面积是梯形COAB面积的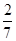 ?
?(3)动点P从点O出发,沿折线OABD的路线移动过程中,设△OPD的面积为S,请直接写出S与
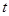 的函数关系式,并写出自变量
的函数关系式,并写出自变量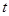 的取值范围。
的取值范围。
(1)设直线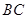 的解析式为
的解析式为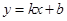 .依题意得:
.依题意得:

解得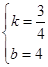
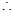 直线
直线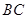 的解析式为
的解析式为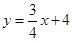 .
.
(2)如图,取OA的中点E,连接DE.

∵D、E分别为梯形OCBA两腰的中点
∴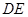 为梯形
为梯形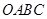 的中位线.
的中位线.
∴DE∥OC∥AB,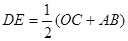
∵OC⊥OA
则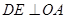 于
于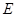
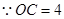 ,
,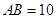 ,
,
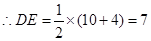 .
.
又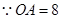 ,
,
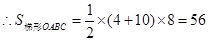 .
.
如图,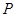 点在
点在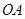 上,且四边形
上,且四边形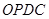 的面积为
的面积为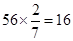 时,
时,
∴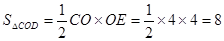 ,
,
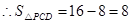 .
.
∴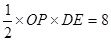 .即
.即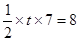
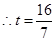 .
.
(3)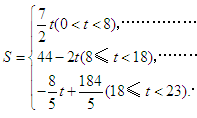
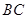 的解析式为
的解析式为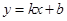 .依题意得:
.依题意得:
解得
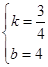
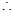 直线
直线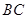 的解析式为
的解析式为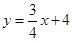 .
. (2)如图,取OA的中点E,连接DE.

∵D、E分别为梯形OCBA两腰的中点
∴
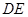 为梯形
为梯形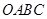 的中位线.
的中位线. ∴DE∥OC∥AB,
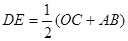
∵OC⊥OA
则
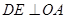 于
于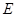
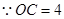 ,
,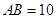 ,
,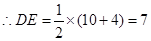 .
. 又
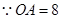 ,
,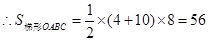 .
. 如图,
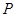 点在
点在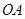 上,且四边形
上,且四边形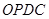 的面积为
的面积为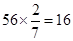 时,
时,∴
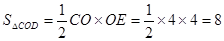 ,
, 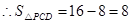 .
.∴
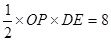 .即
.即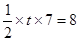
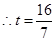 .
. (3)
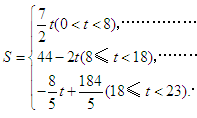
(1)题目给出了B、C点的坐标,可设出直线BC的解析式,应用待定系数法求出解析式即可;
(2)可根据四边形OPDC的面积是梯形COAB面积的 列出方程并解出方程即可;
列出方程并解出方程即可;
(3)要根据P的位置在不同边的具体情况利用相关的知识写出函数关系式及取值范围.
(2)可根据四边形OPDC的面积是梯形COAB面积的
 列出方程并解出方程即可;
列出方程并解出方程即可;(3)要根据P的位置在不同边的具体情况利用相关的知识写出函数关系式及取值范围.

练习册系列答案
相关题目
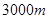 的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加
的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加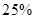 ,结果提前
,结果提前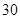 天完成这一任务,实际每天铺设多长管道?
天完成这一任务,实际每天铺设多长管道?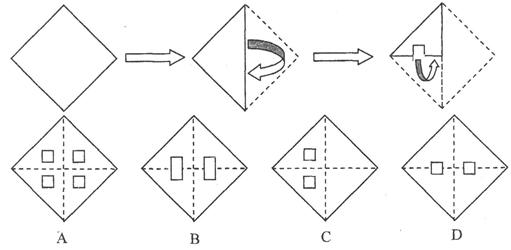
 分别表示学校、小明家、小红家,已知学校在小明家的南偏东
分别表示学校、小明家、小红家,已知学校在小明家的南偏东 ,小红家在小明家正东,小红家在学校北偏东
,小红家在小明家正东,小红家在学校北偏东 ,则
,则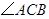 等于( )
等于( )
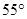
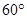

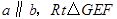 从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中
从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中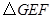 与矩形
与矩形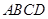 重合部分的面积(S)随时间(t)变化的图象大致是( )
重合部分的面积(S)随时间(t)变化的图象大致是( )

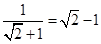 ,
,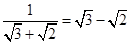 ,
,
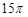
 ,以便在里面配置各种应急药物。现要求该取药点离两个广场入口
,以便在里面配置各种应急药物。现要求该取药点离两个广场入口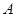 、
、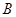 的距离相等,且离观赏点
的距离相等,且离观赏点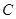 的距离恰好等于
的距离恰好等于