题目内容
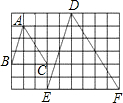
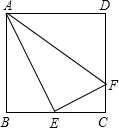
如图，在正方形ABCD中，点E、F分别在BC、CD边上，如果BE=EC，CF=
CD，那么与△ABE相似的三角形是______．
| 1 |
| 4 |
证明：∵四边形ABCD是正方形，
∴∠B=∠C=90°，AB=BC=CD=AD，
∵BE=EC，CF=
CD，
∴AB：BE=2，CE：CF=2，
∴△ECF∽△ABE，
∴∠BAE=∠CEF，
又∵∠BAE+∠BEA=90°，
∴∠CEF+∠BEA=90°，
即∠AEF=90°，
在Rt△CEF中，EF=
CF，
同理可求AE=2
DF，
∴AE：EF=2，
∴△AEF∽△ABE．
故答案是△ECF和△AEF．
∴∠B=∠C=90°，AB=BC=CD=AD，
∵BE=EC，CF=
| 1 |
| 4 |
∴AB：BE=2，CE：CF=2，
∴△ECF∽△ABE，
∴∠BAE=∠CEF，
又∵∠BAE+∠BEA=90°，
∴∠CEF+∠BEA=90°，
即∠AEF=90°，
在Rt△CEF中，EF=
| 5 |
同理可求AE=2
| 5 |
∴AE：EF=2，
∴△AEF∽△ABE．
故答案是△ECF和△AEF．
练习册系列答案
阅读快车系列答案
相关题目
