Question

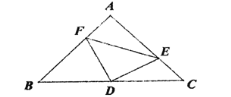
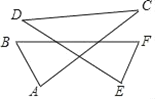
【题目】如图，已知点，分别是的边和延长线上的点，作的平分线，若．

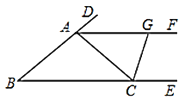
（1）求证：是等腰三角形；

（2）作的平分线交于点，若，求的度数．

Answer 1

【答案】（1）证明过程见解析；（2）70°

【解析】

（1）根据角平分线的性质得到∠DAF=∠FAC，再结合平行线的性质即可得出答案；

（2）根据角平分线的相知得出∠ACG=∠GCE，再根据等腰三角形的性质得出∠BCA和∠ACG，最后结合平行线的性质即可得出答案.

（1）证明：∵AF是∠DAC的角平分线

∴∠DAF=∠FAC

又AF∥BC

∴∠FAC=∠ACB，∠DAF=∠B

∴∠ACB=∠B

∴△ABC是等腰三角形

（2）解：∵CG平分∠ACE

∴∠ACG=∠GCE

又∠B=40°，△ABC是等腰三角形

∴∠BCA =40°

∴∠ACE=180°-∠BCA=140°

∠ACG=∠GCE=∠ACE=70°

∴∠BCG=∠BCA+∠ACG=110°

又AF∥BC

∴∠AGC=180°-∠BCG=70°